Motivations
Contrastive predictive coding (CPC) architecture contains two key steps: 1) generate a global context $c_t$ from former timestamps; 2) discriminate $c_t$ with timestamps $t+k$ in future. Instead of directly predicting future timestamps, CPC takes $c_t$ and $t+k$ in the same time series as positive samples and enlarges the mutual information between them. For $c_t$ and other $t+k$ in different time series, CPC treats them as negative samples and optimize the model by contrastive loss (InfoNCE). In fact, CPC does not leverage the global context $c_t$ adequately. $c_t$ could also be seen as a good source for sampling in contrastive learning.
TS-TCC
TS-TCC is an extension of CPC, which consists of two parallel CPC branches. The architecture of TS-TCC is as follows.
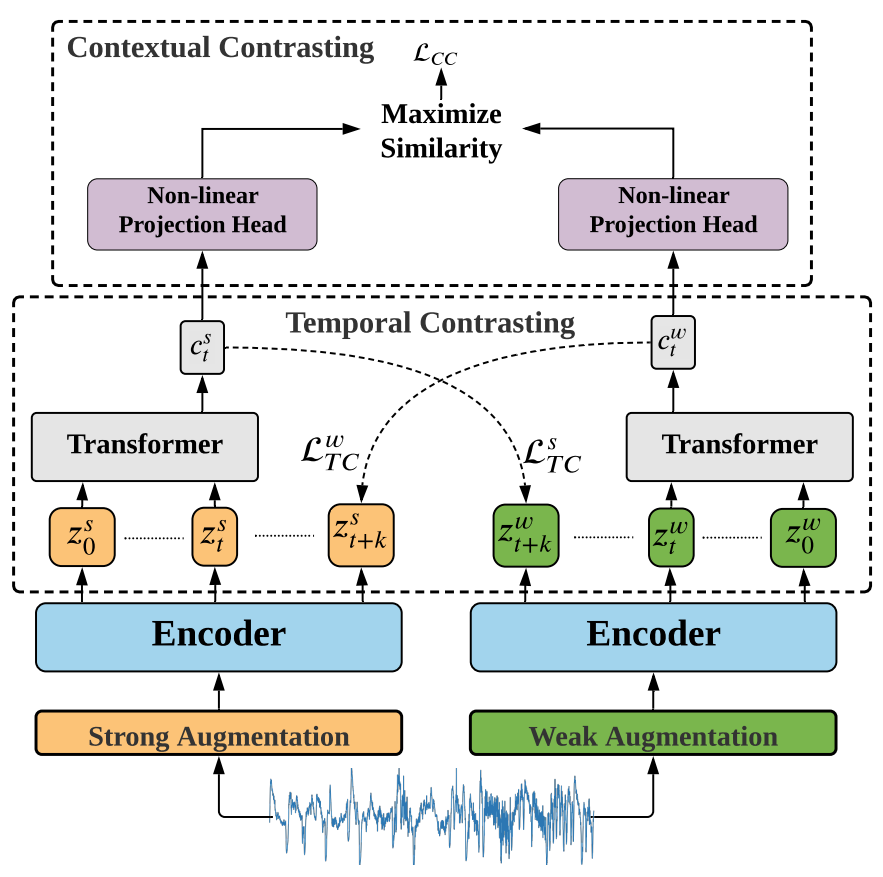
Differing from other prevalent parallel contrastive learning framework, TS-TCC tries to generate two different yet correlated views of the input data based on strong and weak augmentations because the same augmentations family may hinder the performance of the model. Other components are illustrated as below.
- Strong augmentation: permutation-and-jitter strategy, which splits the signal into segments and randomly shuffling them. Then add a random jittering to the permuted signal.
- Weak augmentation: jitter-and-scale strategy, which adds random variations to the signal and scale up its magnitude.
- Encoder: 1D-CNN
- Temporal Contrasting: interactive CPC, whose generator is Transformer (vanilla CPC takes auto-regressive model like LSTM as generator)
- Contextual Contrasting: treat the global context as a new view for two stage contrastive learning
TS-TCC has two contrasting modules to optimize. In this paper, they use two fixed hyperparameters to balance the contribution of temporal and contextual contrastive loss. Future work could dig the relationship among multi-contrastive modules. Besides, we should still consider what transformations applied to time series are more applicable.