Motivations
Data augmentations play an important role in self-supervised learning. Specifically, images are transformed into different views for auxiliary tasks like contrastive learning or mask prediction to obtain a good intermediate representation for downstream tasks. However, we have to admit that it is often unclear which transformations to use. For data other than images, such as time series or tabular data, it is much less well known which transformations are useful, and it is hard to design these transformations manually. Thus, the intuition behind this model NeuTraLAD is to create series of learnable data augmentation and discriminate them.
Here are Some transformations used in this paper: ($M_k$ is a learnable mask)
- feed forward $T_k(x):=M_k(x)$
- residual $T_k(x):=M_k(x)+x$
- multiplicative $T_k(x):=M_k(x)\odot x$
NeuTraL AD
NeuTraL AD is a simple pipeline with learnable data augmentations optimized by a deterministic contrastive loss (DCL) to cope with anomaly detection. Considering data space $\chi$ with samples $D={x^{(i)}\sim\chi}_{i=1}^N$ and $K$ transformations $T:={T_1,\dots,T_K\vert T_k:\chi\rightarrow\chi}$. We assume here that the transformations are learnable with the parameters of transformation $T_k$ by $\theta_k$. DCL encourages each transformed sample $x_k=T_k(x)$ to be similar to its original sample $x$, while encouraging it to be dissimilar from other transformed versions of the same sample, $x_l=T_l(x)$ with $l\not=k$. We define $h(x_k,x_l)$ (in this paper they used cosine similarity) to measure the similarity between $x_k$ and $x_l$. Then DCL is as follows:
\[L_{DCL}=\mathbb{E}_{x\sim D}-\sum_{k=1}^K\log\frac{h(x_k,x)}{h(x_k,x)+\sum_{l\not=k}h(x_k,x_l)}\]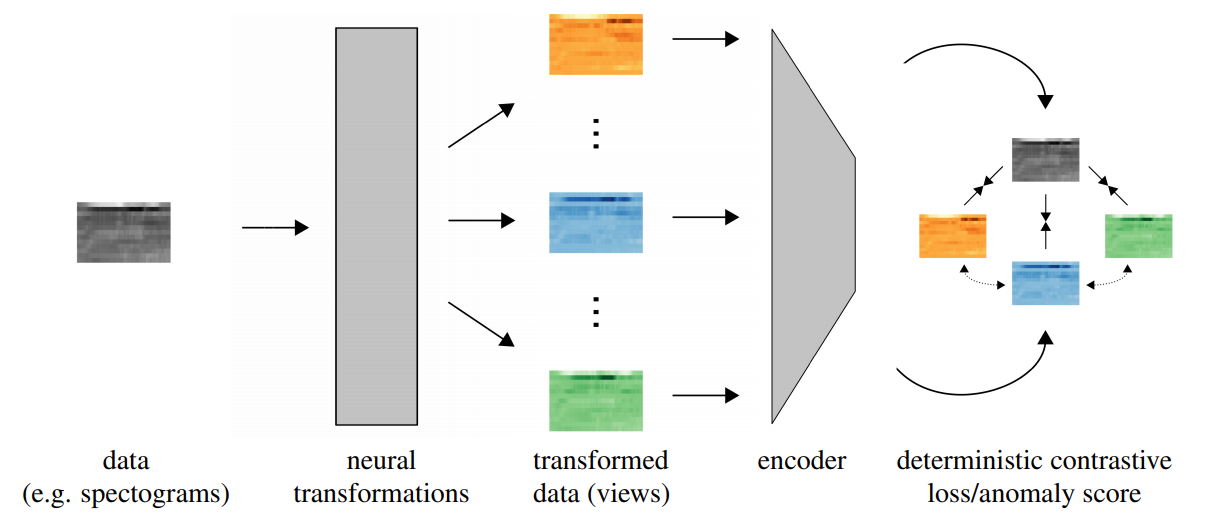
Unlike prevalent parallel contrastive learning framework, NeuTraL AD emphasizes the discrepancy among different transformations. Thus, the positive samples are the original data and its different views; the negative samples are from the same original $x$ with different transformation $T_l$. One advantage of this approach over other methods is that its training loss is also anomaly score. Since the score is deterministic, it can be straightforwardly evaluated for new data points $x$ without original negative samples.
\[S(x)=-\sum_{k=1}^K\log\frac{h(x_k,x)}{h(x_k,x)+\sum_{l\not=k}h(x_k,x_l)}\]The idea of NeuTraL AD is novel because it treats each transformed view as a new class and optimize the model by contrastive loss, which is a little similar to meta-learning. Future work should pay more attention to the discrepancy among different transformation.