Motivations
Traditional time-series forecasting or classification approaches focus on instance-level representations which describe the whole segment of the input time series. In fact, instance-level representations may not be suitable for tasks that require fine-grained features. Multi-scale contextual information with different granularities could improve the generalization capability of learned representations.
Up to now, most of the existing methods have used contrastive loss to capture semantic-level representation on time series. There are three common strategies for constructing positive pairs:
- Subseries consistency: encourages the representation of a time series to be closer its sampled subseries
- Temporal consistency: enforces the local smoothness of representations by choosing adjacent segments as positive samples
- Transformation consistency: augments input series by different transformations, encouraging the model to learn transformation-invariant representations
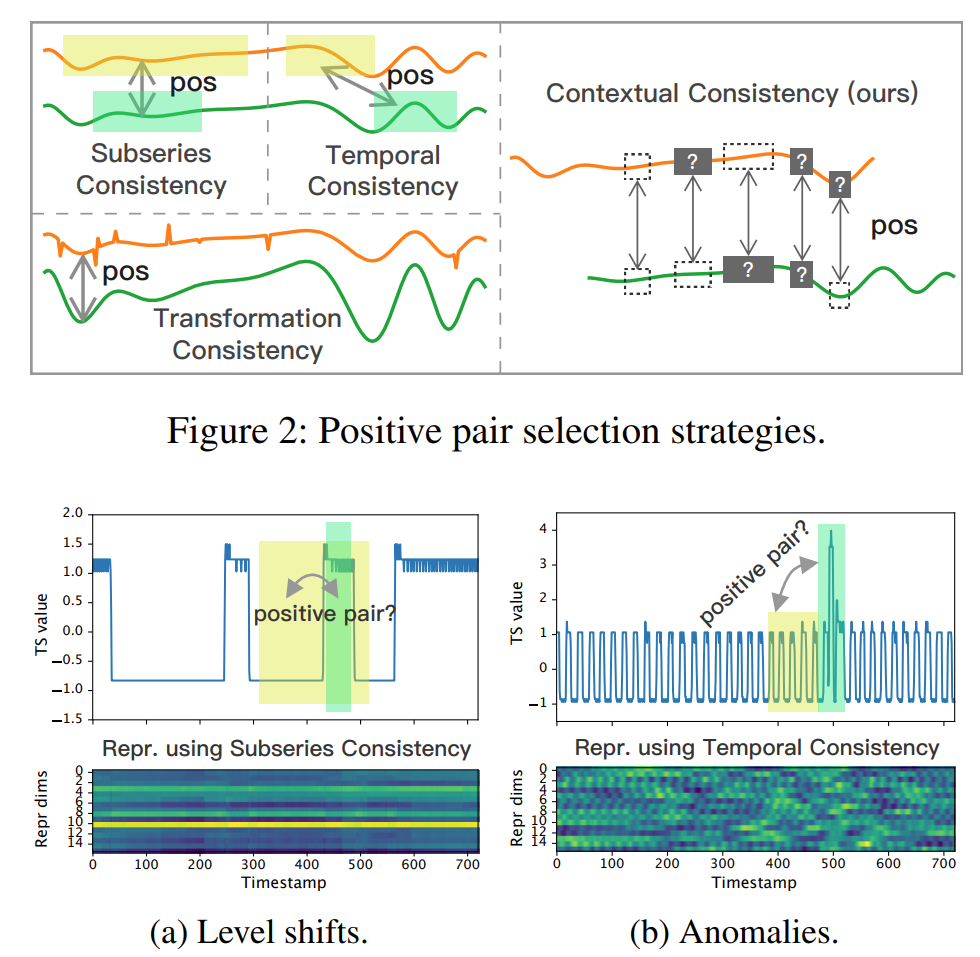
However, subseries consistency is vulnerable when there exist level shifts and temporal consistency may introduce false positive pair when anomalies occur. For transformation, masking and random cropping do not change the magnitude of the time series. Thus, we can treat the representations at the same timestamp in two augmented contexts as positive pairs, which is called contextual consistency.
TS2Vec
Given a set of time series $X={x_1,x_2,\dots,x_N}$ of $N$ instances, our goal is to learn a nonlinear embedding function $f_\theta$ that maps each $x_i$ to its representation $r_i$ that best describes itself. The input time series $x_i$ has dimension $T\times F$, where $T$ is the sequence length and $F$ is the feature dimension. The representation $r_i={r_{i,1},r_{i,2},\dots r_{i,T}}$ contains representation vector $r_{i,t}\in\mathbb{R}^K$ for each timestamp $t$, where $K$ is the dimension of representation vectors.
\[x_i\overset{f_\theta}{\longrightarrow}r_i=\{r_{i,1},r_{i,2},\dots r_{i,T}\}\]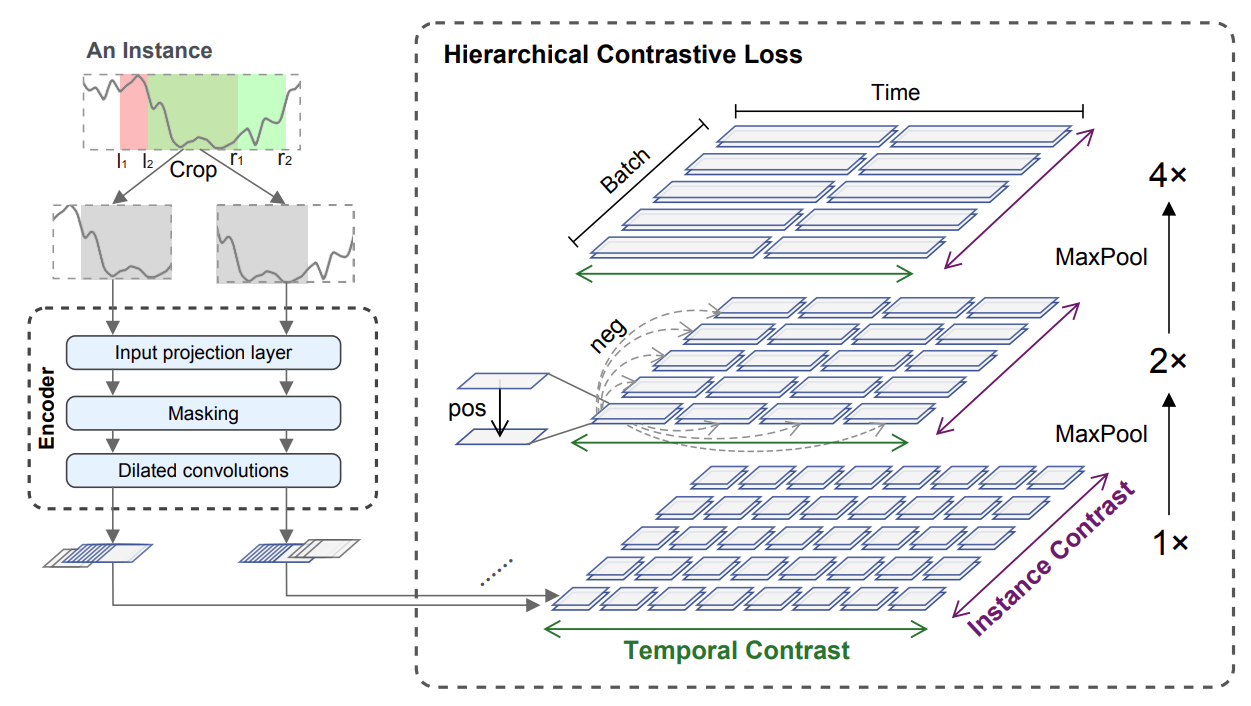
TS2Vec randomly samples two overlapping subseries from an input $x_i$ and feeds them into encoder. Here are three components of the encoder:
- Input projection layer: maps the observation $x_{i,t}$ at timestamp $t$ into a latent vector $z_{i,t}$
- Masking layer: masks $z_i$ with a binary mask which is randomly generated from a Bernoulli distribution with $p=0.5$ along the time axis
- Dilated CNN: extracts the representation at each timestamp
In common practices raw values are directly masked for data augmentation. Notice that $0$ naturally exists in time series. Thus, we choose to mask the latent vector but not raw input.
TS2Vec contains two constructions of sample pairs in contrastive learning:
\[L_{temp}^{(i,t)}=-\log\frac{\exp(r_{i,t}\cdot\acute{r_{i,t}})}{\sum_{\acute{t}\in\Omega}[\exp(r_{i,t}\cdot\acute{r_{i,t}})+\mathbb{I}_{t\not=\acute{t}}\exp(r_{i,t}\cdot r_{i,\acute{t}})]}\] \[L_{inst}^{(i,t)}=-\log\frac{\exp(r_{i,t}\cdot\acute{r_{i,t}})}{\sum_{j=1}^B[\exp(r_{i,t}\cdot\acute{r_{i,t}})+\mathbb{I}_{i\not=j}\exp(r_{i,t}\cdot r_{j,t})]}\] \[L_{dual}=\sum_i\sum_t(L_{temp}^{(i,t)}+L_{inst}^{(i,t)})\]- $r_{i,t}$ and $\acute{r_{i,t}}$ denote the representations for the same timestamp $t$ but from two views of the augmented $x_i$
- Temporal: positive samples are at the same timestamp from two views of the input; negative samples are in the same view at different timestamps
- Instance-wise: negative samples are all the different instances in the mini-batch at the same view and timestamp

Hierarchical features are extracted by the contrastive loss with the pooling operation. The following figure shows the effect of all the components. Augmentations tell us that we should consider how to design proper feature-invariant transformation applied to time series.
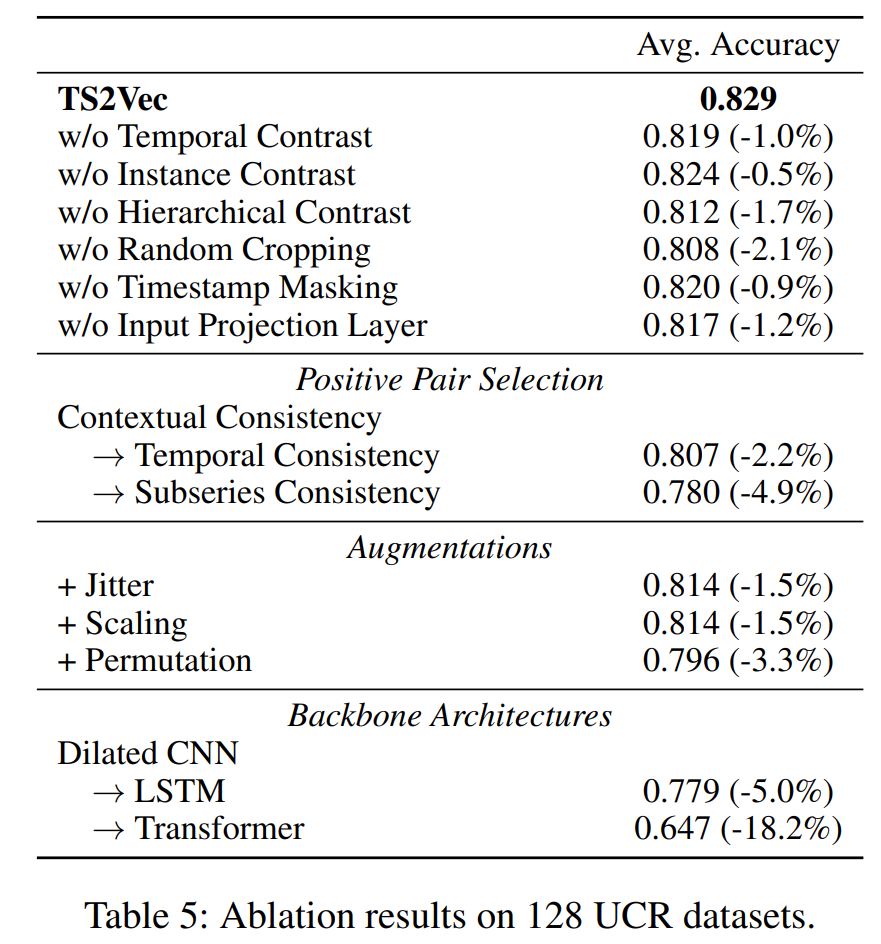
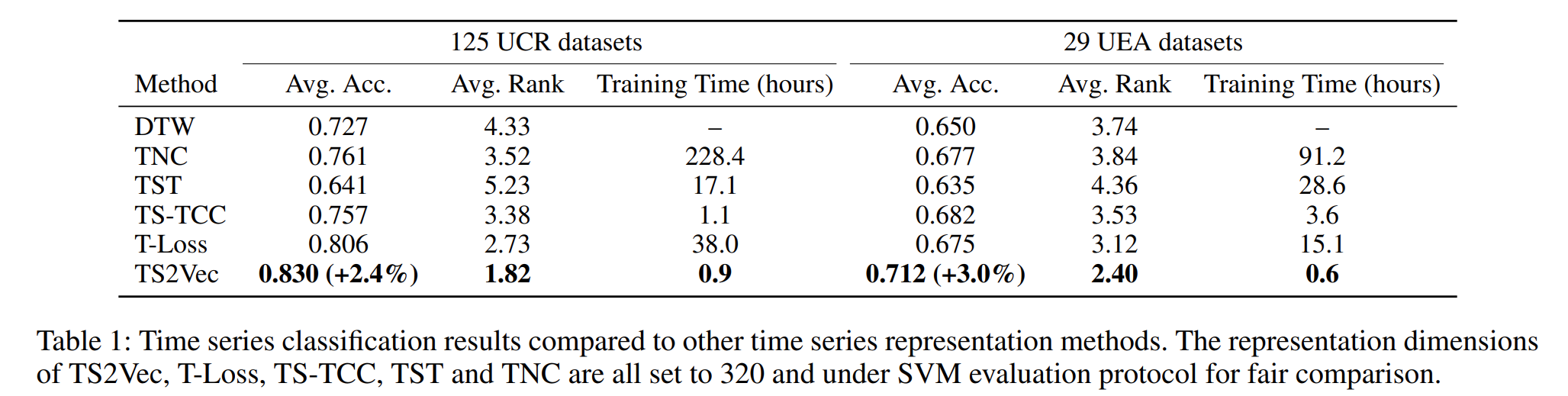
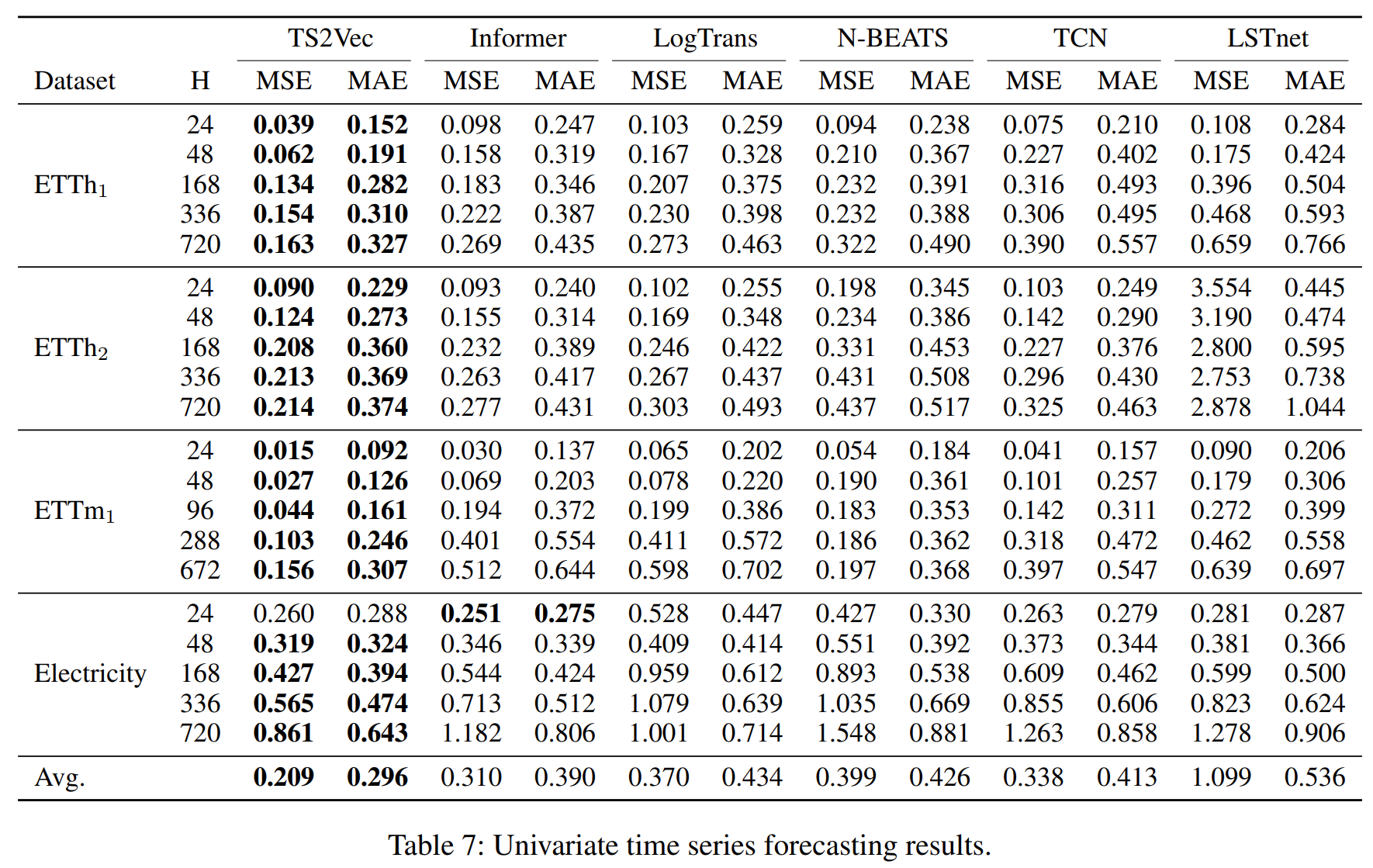
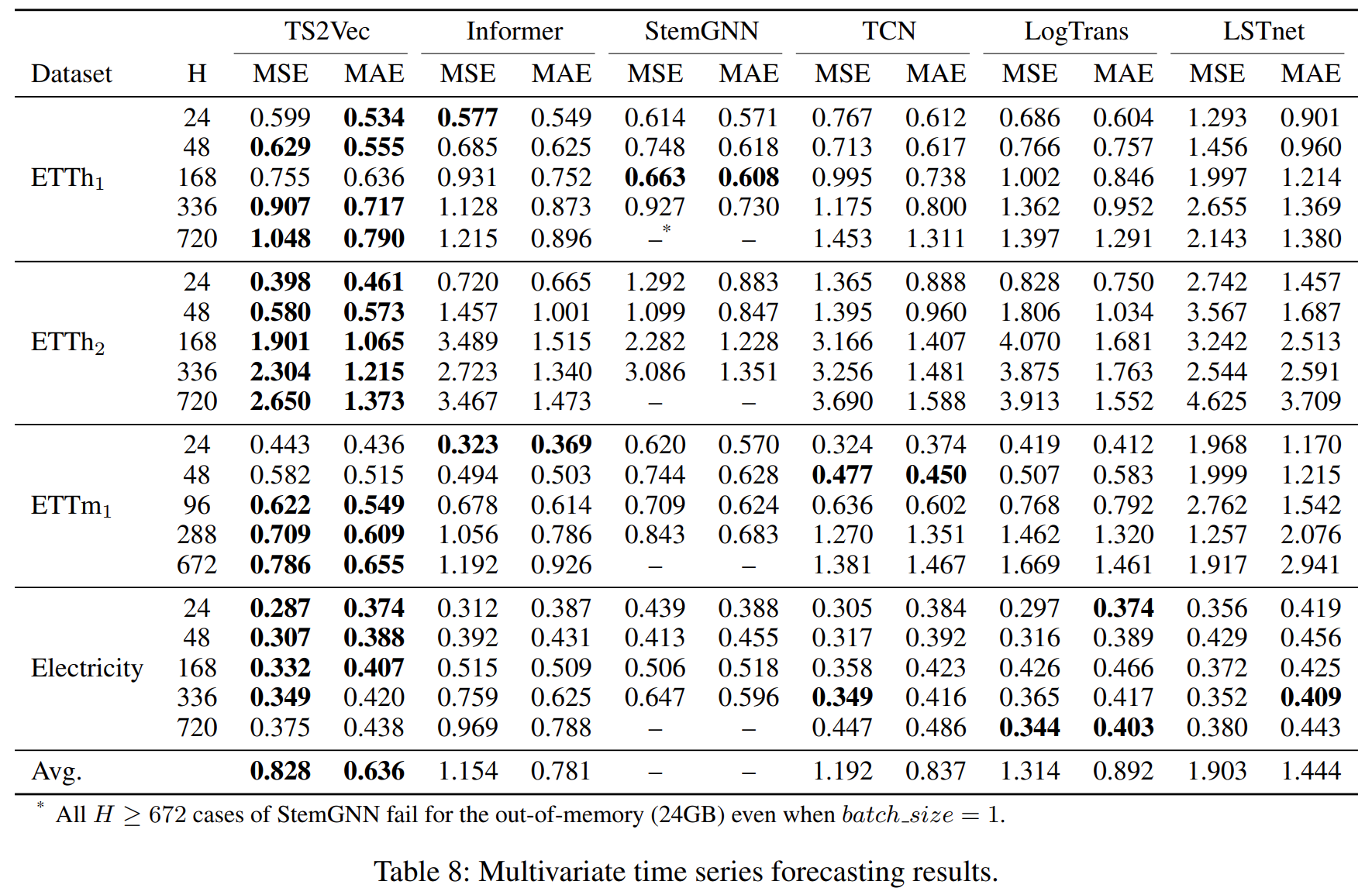
The following tables present the results of TS2Vec compared with other existing methods of unsupervised learning on UCR, UEA and ETT.