Background and Motivation
Recommended: Contrastive Self-Supervised Learning
- Defects in supervised learning:
- The underlying data has a much richer structure than what sparse labels or rewards could provide. Thus, purely supervised learning algorithms often require large numbers of samples to learn from, and converge to brittle solutions.
- We can’t rely on direct supervision in high dimensional problems, and the marginal cost of acquiring labels is higher in problems like RL.
- It leads to task-specific solutions, rather than knowledge that can be repurposed.
- Key: how to model a better representations from raw observations?
- Intuition: to learn the representations that encode the underlying shared information between different parts of the (high-dimensional) signal. At the same time it discards low-level information and noise that is more local.
- Approach: Maximize mutual information but not conditional probability $p(x\vert c)$ to get a better encoded representation
Contrastive Predictive Coding (CPC)
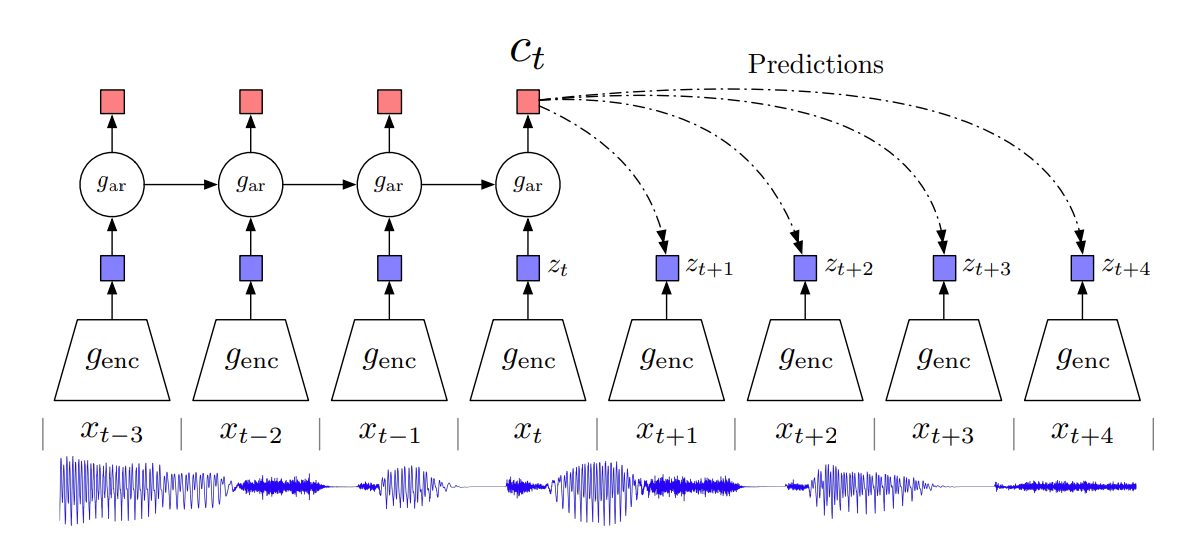
- Applicable to sequential data
- $g_{enc}$ : a non-linear encoder mapping input sequence $x_t$ to $z_t$
- $g_{ar}$ : an autoregressive model which summarizes all $z_{\leq t}$ to produce a context latent representation $c_t$
- $f_k$ is modeled to preserve the mutual information between $x_{t+k}$ and $c_t$
Given a set $X={x_1,\dots,x_N}$ of $N$ random samples containing one positive sample from $p(x_{t+k}\vert c_t)$ and $N-1$ negative samples from $p(x_{t+k})$, we optimize:
\[L_N=-\mathbb{E}(\log\frac{f_k(x_{t+k},c_t)}{\sum_{x_j\in X}f_k(x_j,c_t)})\]Optimizing $L_N$ is equivalent to maximizing the mutual information between $x_{t+k}$ and $c_t$
\[p(d=i\vert X,c_t)=\frac{p(d=i,X\vert c_t)}{p(X\vert c_t)}=\frac{p(x_i\vert c_t)\prod_{k\not=i}p(x_k)}{\sum_jp(x_j\vert c_t)\prod_{k\not=j}p(x_k)}=\frac{\frac{p(x_i\vert c_t)}{p(x_i)}}{\sum_j\frac{p(x_j\vert c_t)}{p(x_j)}}\] \[I(x_{t+k},c_t)\geq\log N-L_N\]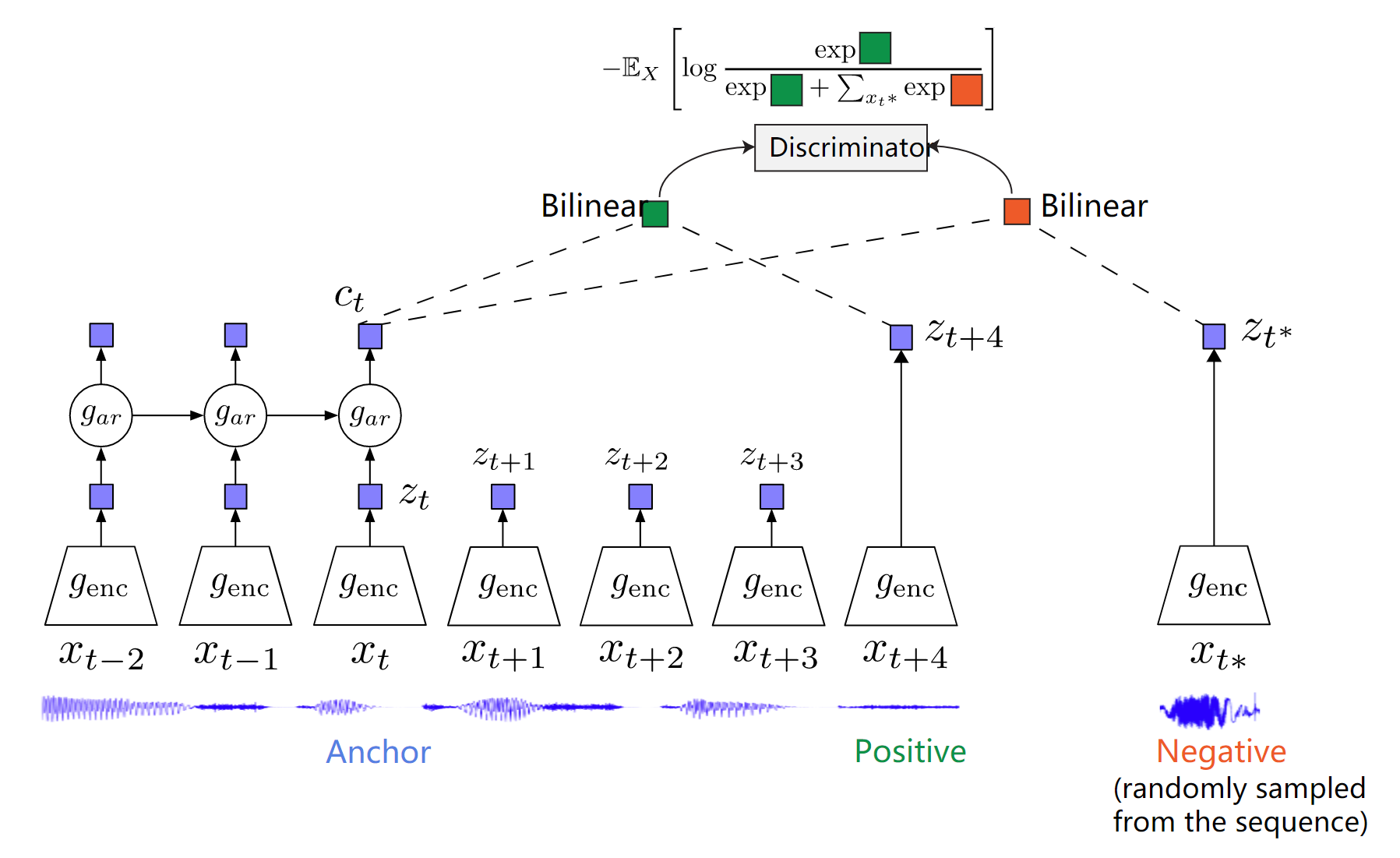
1 | |