ResNet

Is learning better networks as easy as stacking more layers?

Overview

• Q1: Why do we need a deeper network?
• A: CNN can extract low/mid/high-level features through different filters, which means the deeper network is, the more features we can extract.
• Q2: Why not simply add more and more layers to networks?
• A: On the one hand it will cause a vanishing/exploding gradient (addressed by normalized initialization/BN)，on the other hand, we can’t ignore the degradation (with the network depth increasing, accuracy gets saturated and then degrades rapidly).
  

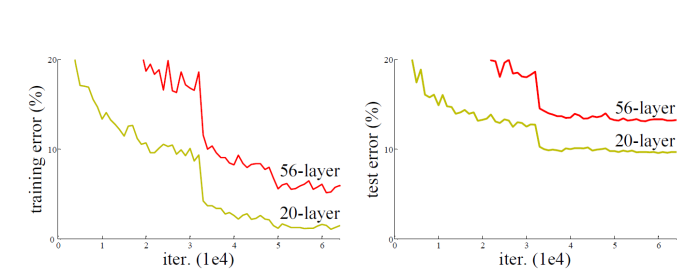
Experiments

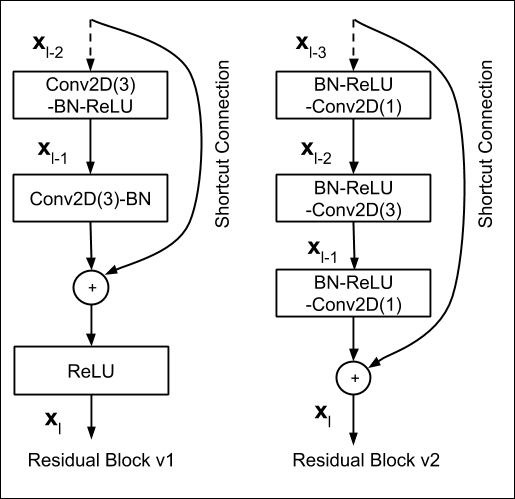
  The authors deepen the model by adding identity mapping layers, and it is abnormal that the deep model is worse than the shallow one. However, it is hard for the solvers to approximate identity mapping by multiple non-linear layers in practice. Denoting the desired underlying mapping as $H(x)$, the stacked non-linear layers aim to fit $F(x)$. By adding $x$ (realized by shortcut connection), the model is prone to fit $F(x)$ rather than $H(x)$.

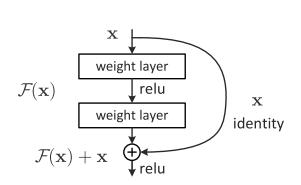
  I suppose that the residual function vanishes the error accumulated to some extent, which is similar to some methods in numerical calculation. The $x$ can fully be transmitted to the next layer.