概率论（probability theory）

样本空间（sample space）

概率描述的是相对频率，用以研究相继发生或同时发生的大量事件的平均特性。贝特朗投针实验告诉我们，探讨某一事件概率的前提是确定样本空间，不同的样本空间所对应的事件概率可能是不同的。一般来说，随机试验的所有样本点组成的集合 $S$ 称为样本空间，样本空间的任意子集称为随机事件。

例 1：工人生产三个零件，以事件 $A_i(i=1,2,3)$ 表示他生产的第 $i$ 个零件是合格品，那么

事件	结果表示
至少有一个合格品	$A_1\cup A_2\cup A_3$
最多只有两个合格品	$\overline{A_1A_2A_3}$

现代概率论的基础是苏联数学家柯尔莫格罗夫提出的公理化定义（axiom），结合集合论我们很容易就能得出诸如差事件或容斥定理那样的概率论公式。

任意事件 $A$ 满足 $P(A)\geq0$
必然事件的概率为一，即 $P(S)=1$
互斥事件 $A,B$ 满足 $P(A\cup B)=P(A)+P(B)$

在假定事件 $B$ 发生的情况下，事件 $A$ 发生的概率称为条件概率（conditional probability），记作 $P(A\vert B)$。条件概率相当于对原始样本空间进行了缩减，将 $S$ 简化为由 $B$ 事件组成的子集，因此适用于普通概率的公式同样也适用于条件概率。

\[P(A\vert B)=\frac{P(AB)}{P(B)},\quad P(B)\ne0\]

进一步，若 ${A_1,A_2,\dots,A_n}$ 是 $S$ 的分割（division），我们可以写出任意事件 $B$ 基于该分割的展开式，该式是全概率定理（total probability theorem）的表现形式。

\[P(B)=\sum_{i=1}^n{P(A_i)P(B\vert A_i)}\]

结合条件概率和全概率公式我们可以推导出著名的贝叶斯定理（Bayes’ theorem），它的一般形式如下，其中 $H$ 表假设（hypothesis），$E$ 表事实（evidence）。

\[P(H\vert E)=\frac{P(H)P(E\vert H)}{P(E)}=\frac{P(H)P(E\vert H)}{P(H)P(E\vert H)+P(\bar{H})P(E\vert\bar{H})}\]

“New evidence does not completely determine your beliefs in a vaccum, it should update prior beliefs.”

贝叶斯定理的内核如上述所言，我们对样本空间 $S$ 提出了假设 $H$，根据新的事实 $E$ 对假设进行更新（update），这里 $E$ 同样起到了缩减样本空间的作用。$P(H)$ 称为先验概率（prior），$P(E\vert H)$ 称为似然概率（likelihood），$P(H\vert E)$ 称为后验概率（posterior）。

例 2：有 $n$ 枚硬币，$n-1$ 枚是均匀的，一枚两面都是正面，随机选一枚掷 $m$ 次都是正面，求选择的这枚硬币是均匀的概率。

\[P(H)=\frac{n-1}{n}\quad P(E\vert H)=\frac{1}{2^m}\] \[P(E)=\frac{n-1}{n}\times\frac{1}{2^m}+\frac{1}{n}\times1=\frac{2^m+n-1}{n\cdot2^m}\] \[P(H\vert E)=\frac{P(H)P(E\vert H)}{P(E)}=\frac{n-1}{2^m+n-1}\]

例 3：医院检测一项疾病，当地经排查得知该病的患病率为 $2\%$。已知这个检查诊断正确率为 $95\%$（即得病的人中有 $5\%$ 概率漏诊，没病的人有 $5\%$ 误诊），此时我们发现了一个人检测为阳性，问此人患病的概率。

\[P(H)=0.02\quad P(E\vert H)=0.95\] \[P(E)=0.02\times0.95+0.98\times0.05=0.068\] \[P(H\vert E)=\frac{P(H)P(E\vert H)}{P(E)}=0.279\]

试剂的准确率主要源自患病人群的筛查，因此 $E$ 的引入修正了我们对样本空间的错误认知。针对更广泛的群体，试剂的高灵敏度一定伴随着部分假阳性问题，所以对于传染性疾病复检是很有必要的。

有时候我们会关心多个事件同时或连续进行（取交集）的概率，因此我们需要引入事件独立性的概念。独立事件 $A,B$ 满足 $P(AB)=P(A)P(B)$，意及两事件间互不影响，注意独立与互斥没有必然联系。

例 4：掷一枚不均匀硬币 $n$ 次，求出现 $k$ 次正面的概率（单次正面概率为 $p$）。

\[P=\binom{n}{k}p^k(1-p)^{n-k}\]

这是一个经典的 $n$ 重伯努利试验（Bernoulli experiment），它描述了 $n$ 次独立实验中事件 $A$ 成功或失败次数的分布情况。

随机变量（random variable）

一维随机变量及其分布

随机变量是样本空间 $S$ 上的函数 $f:S\rightarrow\mathbb{R}$ ，记为 $X(s)$，$s\in S$。随机变量的分布函数（probability distribution function）定义为 $F(x)=P{X\leq x}$，描述了随机变量落入某特定区间的概率，它满足以下性质：

分布函数非减，且处处右连续
$F(-\infty)=0$，$F(+\infty)=1$
$P{a<X\leq b}=F(b)-F(a)$，$P{X=x_0}=F(x_0)-F(x_0-0)$

分布函数描述了随机变量 $X$ 的统计性质，分布函数的导数被称为概率密度函数（probability density function），记作 $f_X(x)$。

\[f_X(x)=\frac{\mathrm{d}F(x)}{\mathrm{d}x}\qquad F(x)=\displaystyle\int_{-\infty}^xf_X(t)\mathrm{d}t\]

显然连续型随机变量的分布函数必为连续函数，而离散型随机变量的分布函数呈阶跃函数，因此其密度函数可用冲激函数表示，这就是随机信号分析中的概率质量函数（probability mass function）。

\[f_X(x)=\sum_ip_i\delta(x-x_i)\]

离散型随机变量中最简单的是伯努利随机变量，$X$ 仅取两个值 $0,1$。$n$ 重伯努利试验的结果就可以用二项分布（binomial distribution）来描述，而泊松分布即二项分布的极限情况，它描述了大量实验中稀有事件发生的次数分布。

\[P\{X=k\}=\displaystyle\binom{n}{k}p^k(1-p)^{n-k}\] \[P\{X=k\}=\displaystyle\frac{\lambda^k}{k!}e^{-\lambda}\]

有时我们会关注 $n$ 重伯努利试验至第一次成功所需的实验次数（例如掷骰子何时会出现 $6$），这可以用几何分布（geometric distribution）来描述。若假定前 $m$ 次没有成功，第一次成功出现在接下来的 $n$ 次试验的概率仅依赖 $n$，这说明几何分布具有无记忆性。

\[P\{X=k\}=(1-p)^{k-1}p\quad k=1,2,\dots\] \[E(X)=\sum_{k=1}^\infty kP\{X=k\}=\frac{1}{p}\] \[P\{X>m\}=\sum_{k=m+1}^\infty (1-p)^{k-1}p=(1-p)^m\] \[P\{X>m+n\vert X>m\}=\frac{P\{X>m+n\}}{P\{X>m\}}=(1-p)^n\]

几何分布的一个显而易见的推广是考虑实现 $r$ 次成功所需的实验次数（例如掷两次 $6$ 所需的掷骰子次数），这可以用负二项分布（negative binomial distribution）来描述。考虑到几何分布的无记忆性，我们可以将负二项分布拆解为 $r$ 个几何分布实验的和，因此负二项分布的期望和方差可以直接从几何分布推出。

\[P\{X=k\}=\binom{k-1}{r-1}p^{r}(1-p)^{k-r}\quad k=r,r+1,\dots\] \[E(X)=\frac{r}{p}\]

倘若读者饶有兴致的画出随着 $n$ 增大时 $n$ 重伯努利试验的概率分布，你会惊奇的发现所画出的曲线会慢慢逼近于一个钟型分布曲线，这就是概率论历史上最为著名的正态分布（normal distribution）曲线。（推荐阅读：正态分布的前世今生）

\[f_X(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]

高斯在探究测量问题中的误差分布时使用最大似然估计得出了正态分布的一个简洁的证明。首先介绍最大似然估计，一般的，设总体 $X$ 的概率分布为 $f(x;\theta)$，$\theta$ 为未知参数，$X_1,X_2,\dots,X_n$ 是从该总体中抽取的样本，则它们的联合概率分布为：

\[L(\theta)=L(x_1,x_2,\dots,x_n;\theta)=\prod_{i=1}^nf(x_i;\theta)\]

$L(\theta)$ 即 $\theta$ 的似然函数（likelihood function），所谓最大似然估计，即利用概率最大的事件最有可能出现这一想法，用样本 $x_1,x_2,\dots,x_n$ 估计未知参数 $\theta$，对 $L(\theta)$ 求导数即可得出 $\theta$ 的最大似然估计值。

\[\hat{\theta}=\text{argmax}(L(x_1,x_2,\dots,x_n;\theta))\]

记未知参数 $\theta$ 为真值，$x_1,x_2,\dots,x_n$ 为 $n$ 次独立测量值，假设误差分布为 $f(x)$，则测量值对应的误差的联合概率可记为：

\[L(\theta)=L(x_1,x_2,\dots,x_n;\theta)=\prod_{i=1}^nf(x_i-\theta)\] \[\frac{\partial\log L(\theta)}{\partial\theta}=0\Rightarrow\sum_{i=1}^n\frac{f'(x_i-\theta)}{f(x_i-\theta)}=0\]

记 $g(x)=\displaystyle\frac{f’(x)}{f(x)}$，则有 $\displaystyle\sum_{i=1}^ng(x_i-\theta)=0$。高斯假设最大似然估计的解应当是测量值的算术平均，代入上式即有 $\displaystyle\sum_{i=1}^ng(x_i-\bar{x})=0$。

考虑到测量的任意性，对 $n$ 取不同的特值即可得到关于 $g(x)$ 的种种性质，而满足这些性质的唯一的连续函数就是 $g(x)=cx$，因此有：

\[\frac{f'(x)}{f(x)}=cx\Rightarrow f(x)=Me^{cx^2}\]

由于 $f(x)$ 是概率密度函数，对 $f(x)$ 做正规化处理即可得到 $N(0,\sigma^2)$。事实上，如果固定一个分布函数的均值和方差，那么正态分布就是熵最大的概率分布。

统计特征（statistical characteristics）

随机变量刻画了样本空间内所有事件取值的可能性，因此事件的统计特征（如均值）即可用随机变量的统计特征来描述。随机变量 $X$ 的期望（expectation）定义如下：

\[E(X)=\int_{-\infty}^\infty xf_(x)\mathrm{d}x=\lim_{\Delta\rightarrow0}\sum_{k=-\infty}^\infty x_kf(x_k)\Delta x=\int_SX\mathrm{d}P\]

冷知识：熵可以看做是信息量的期望，$H(x)=-\displaystyle\int_Sp(x)\log p(x)\mathrm{d}x$

期望描述了大量事件发生时的平均特性，黎曼和（Riemann sum）告诉我们，当实验次数 $n\rightarrow\infty$ 时，随机变量观测值的算数平均值趋向于期望。事实上，期望可看做样本空间内所有子事件与之概率（测度）之积的和，即 $X$ 的勒贝格积分（Lebesgue integral）。容易证明，期望的计算是满足线性性质的。

\[E(aX+bY)=aE(X)+bE(Y)\]

方差（variance/deviation）描述了随机变量与其期望的偏离/集中程度，方差越大偏离程度越大。（无特殊说明，我们习惯用 $\mu$ 表示均值）

\[D(X)=E((X-\mu)^2)=\int_{-\infty}^\infty (x-\mu)^2f_(x)\mathrm{d}x\]

如果把 $f(x)$ 解释为概率在 $x$ 轴上的质量分布函密度，那么 $E(X)$ 就是它的重心，$E(X^2)$ 是它对原点的惯性矩，$D(X)$ 则是其对重心的转动惯性矩，标准差 $\sigma$ 表示回转半径。期望和方差仅仅给出了 $f(x)$ 的一些特性，其他性质则隐藏在其他的矩（moment）信息里。以下给出了常用的 $n$ 阶矩和 $n$ 阶中心距（central momen）的公式，注意期望实质就是 $f(x)$ 的一阶矩，而方差是其的二阶中心距。

\[m_n=E(X^n)=\int_{-\infty}^\infty x^nf(x)\mathrm{d}x\] \[\mu_n=E((X-E(X))^n)=\int_{-\infty}^\infty(x-E(X))^nf(x)\mathrm{d}x\]

对概率密度函数做共轭傅里叶变换就可以用密度函数的 $n$ 阶矩特征来表示其性质，注意 $\Phi(\omega)$ 在原点的导数等于 $X$ 的各阶矩，因此 $\Phi(\omega)$ 又被称为矩函数。

\[\Phi_X(\omega)=\int_{-\infty}^\infty f(x)e^{j\omega x}\mathrm{d}x=E(e^{j\omega x})\] \[E(e^{j\omega x})=1+\frac{j\omega E(X)}{1!}+\frac{(j\omega)^2E(X^2)}{2!}+\dots+\frac{(j\omega)^nE(X^n)}{n!}\] \[f(x)=\frac{1}{2\pi}\int_{-\infty}^\infty\Phi_X(\omega)e^{-j\omega x}\mathrm{d}\omega\qquad\Phi^{(n)}(0)=m_n\]

例 5（卷积定理）：已知 $X,Y$ 是独立的随机变量，且 $Z=X+Y$，求 $Z$ 的概率密度函数。

\[\Phi_Z(\omega)=\Phi_X(\omega)\cdot\Phi_Y(\omega)\] \[f_Z(z)=f_X(x)*f_Y(y)\]

可以见得，特征函数的引入大大简化了复合型随机变量的运算，原本多个独立随机变量的和需要进行复杂的卷积运算，而转换为特征函数后只需进行简单的乘积然后进行反变换即可得出结果。由于傅里叶变换中变换前后的函数一一对应，因此对于 $Y=g(X)$ 类随机变量仅需通过配凑的方式即可得出密度函数。

例 6：已知 $X\sim N(0,1)$，$Y=X^2$，求 $f_Y(y)$。

\[\Phi_Y(\omega)=\int_{-\infty}^\infty f(x)e^{j\omega x^2}\mathrm{d}x=\frac{2}{\sqrt{2\pi}}\int_0^\infty e^{j\omega y}e^{-\frac{y}{2}}\frac{1}{2\sqrt{y}}\mathrm{d}y\] \[f_Y(y)=\frac{1}{\sqrt{2\pi y}}e^{-\frac{y}{2}}U(y)\]

二维随机变量及其分布

\[F(x,y)=P\{X\leq x,Y\leq y\}\qquad f(x,y)=\frac{\partial^2F(x,y)}{\partial x\partial y}\] \[P\{(X,Y)\in D\}=\displaystyle\iint_Df(x,y)\mathrm{d}x\mathrm{d}y\]

二维随机变量的联合分布函数和密度函数与一维相仿，注意我们在关注多随机变量联合分布的同时，也会格外关注单个随机变量的统计特性。

\[f_X(x)=\int_{-\infty}^\infty f(x,y)\mathrm{d}y\qquad f_Y(y)=\int_{-\infty}^\infty f(x,y)\mathrm{d}x\]

二维随机变量的密度函数同样可看做 $\mathbb{R}^2$ 上的质量密度函数，期望同样表质心，相关矩的性质也与一维一致。

例 7：已知 $f(x,y)=1$，$0<y<x<1$，其他情况为 $0$，求 $E(X\vert Y)$ 和 $E(Y\vert X)$。

\[f_X(x)=\int_0^x1\mathrm{d}y=x\qquad f_Y(y)=\int_y^11\mathrm{d}x=1-y\] \[f(x\vert y)=\frac{1}{1-y}\qquad f(y\vert x)=\frac{1}{x}\] \[E(X\vert Y)=\int_{-\infty}^\infty xf(x\vert y)\mathrm{d}x=\int_y^1\frac{x}{1-y}\mathrm{d}x=\frac{1+y}{2}\] \[E(Y\vert X)=\int_{-\infty}^\infty yf(y\vert x)\mathrm{d}y=\int_0^x\frac{y}{x}\mathrm{d}y=\frac{x}{2}\]

事实上 $E(Y\vert X)$ 描述了 $(x,x+\mathrm{d}x)$ 这个垂直带状质量密度函的质心轨迹，该轨迹又被称为回归线。

例 8：$Z=X/Y$，求 $F_Z(z)$。

\[P\{X/Y\leq z\}=P\{X\leq YZ,Y>0\}+P\{X\geq XY,Y<0\}\] \[F_Z(z)=\int_0^\infty\int_{-\infty}^{yz}f(x,y)\mathrm{d}x\mathrm{d}y+\int_{-\infty}^0\int_{yz}^\infty f(x,y)\mathrm{d}x\mathrm{d}y\]

上例给出了形如 $Z=g(X,Y)$ 的复合型随机变量分布函数的求法，对于和式我们可以用卷积定理简单求解，对于更一般的情况我们采取分割概率空间的情况分别求积分。

例 9：$Z_1=\max(X,Y)$，$Z_2=\min(X,Y)$，求 $F_{Z_1}(z)$ 和 $F_{Z_2}(z)$。

\[F_{Z_1}(z)=P(X\leq z,Y\leq z)=F_X(z)\cdot F_Y(z)\] \[F_{Z_2}(z)=1-P\{X>z,Y>z\}=F_X(z)+F_Y(z)-F_{XY}(z,z)\]

有时候我们会关注随机变量间的关系。独立性 $F(x,y)=F_X(x)F_Y(y)$ 说明了事件 $X,Y$ 互不影响，而相关性（correlation）则从空间上给出了事件间的位置关系。将随机变量抽象为向量，则 $E(XY)$ 可看做 $X,Y$ 的内积，柯西不等式在随机变量上的表现形式即：

\[E^2(XY)\leq E(X^2)E(Y^2)\]

定义协方差（covariance）$C(X,Y)$ 描述随机变量去均值后的位置关系，是两个随机变量间线性关系强弱的一种度量，协方差为零则表示去均值后的随机变量相互正交（orthogonal），即不相关。相关系数 $\rho_{XY}$ 将协方差规范至 $[0,1]$ 上的实数。

\[C(X,Y)=E((X-E(X))(Y-E(Y)))=E(XY)-E(X)E(Y)\] \[\rho_{XY}=\frac{C(X,Y)}{D(X)D(Y)}\]

注意随机变量间独立则一定不相关，反之不成立。

大数定律和中心极限定理

在统计活动中，人们发现，在相同条件下大量重复进行一种随机试验时，事件发生的频率值会趋近于某一数值，这个就是最早的大数定律，即频率以某种意义收敛于概率。

lemma 1：定义示性函数（indicator function）$I_{(A)}$，其在事件 A 成立时返回 $1$，否则为 $0$，它满足以下性质：

\[E(I_{(A)})=P\{A\}\qquad I_{(x\geq a)}\leq\frac{X}{a}\]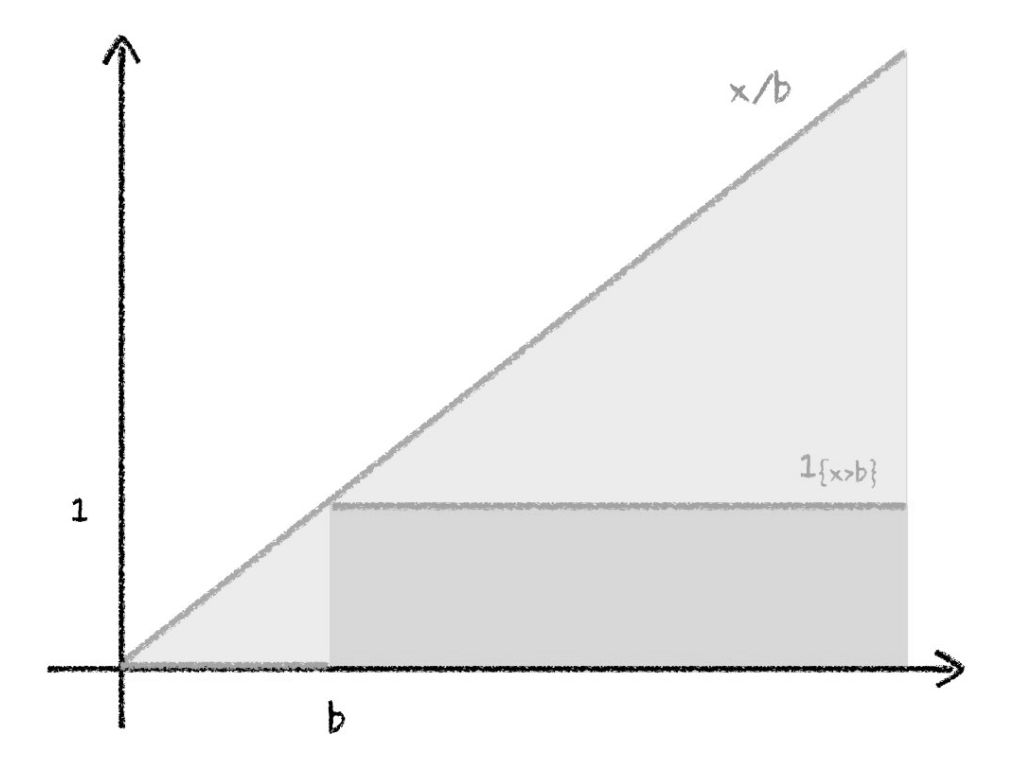

将自变量 $x$ 替换为随机变量 $X$，对两边取均值即可得到马尔科夫不等式（Markov inequality）。

\[P\{X\geq a\}\leq\frac{E(X)}{a}\]

对于切比雪夫不等式（Chebyshev’s theorem），也可以用类似的示性函数在几何角度上直观证明。对于任意的 $x,a,b$，我们有：

\[I_{(\vert x-a\vert\geq b)}\leq\frac{(x-a)^2}{b^2}\]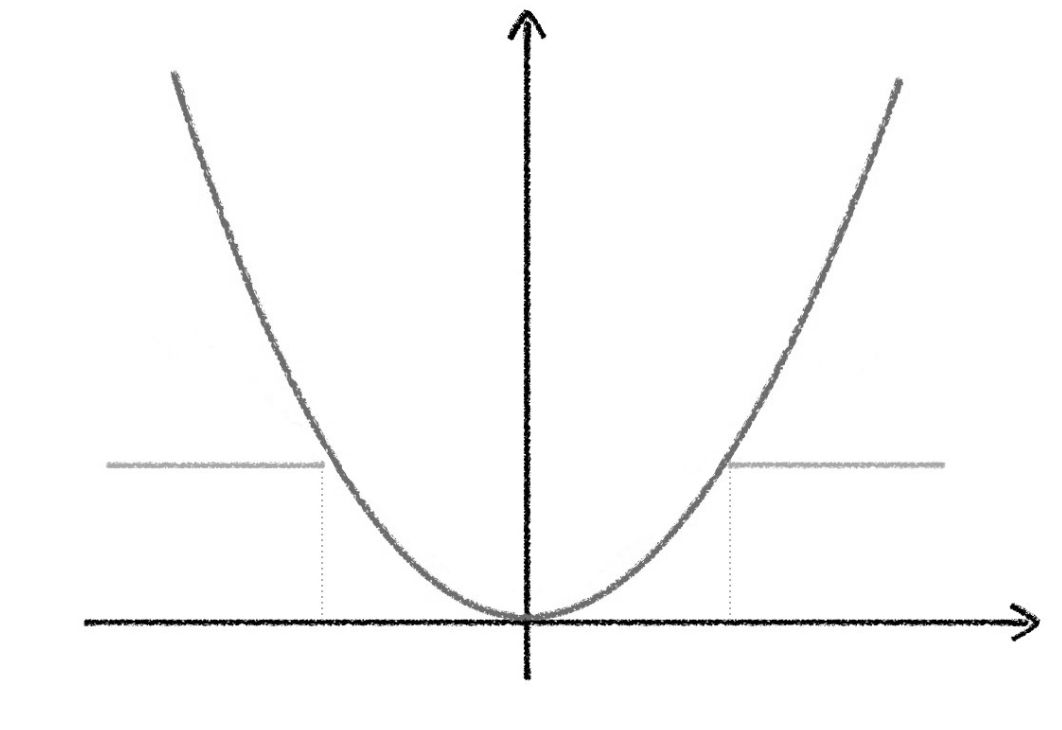

选取随机变量的均值作为 $a$ ，注意到 $D(X)=E((X-\mu)^2)$，对不等式两边取均值，对于任意正数 $\epsilon$，我们有：

\[P\{\vert X-E(X)\vert\geq\epsilon\}\leq\frac{D(X)}{\epsilon^2}\]

切比雪夫不等式基于方差给出了随机变量取值与样本均值间偏差可能性的上界，它是证明一系列大数定律的一把利刃。

lemma 2：定义随机变量序列 $X_1,X_2,\dots,X_n$，若存在随机变量 $X$，使得对于任意 $\epsilon>0$，有：

\[\lim_{n\rightarrow\infty}P\{\vert X_n-X\vert<\epsilon\}=1\]

则称序列 $X_1,X_2,\dots,X_n$ 依概率收敛于 $X$，简记为 $X_n\overset{P}{\longrightarrow}X$。

theorem 1（切比雪夫大数定律）：设 $X_1,X_2,\dots,X_n$ 是两两不相关的随机变量序列，且方差有界，记该序列的算术平均值为 $Y_n$，则 $Y_n\overset{P}{\longrightarrow}E(Y_n)$。

\[0\leq\lim_{n\rightarrow\infty}P\{\vert Y_n-E(Y_n)\vert\geq\epsilon\}\leq\lim_{n\rightarrow\infty}\frac{D(Y_n)}{\epsilon^2}=0\]

theorem 2（伯努利大数定律）：在 $n$ 重伯努利实验中，设单次实验事件 A 发生的概率为 $p$，$\mu_n$ 为 $n$ 重伯努利实验中事件 A 发生的次数，则 $\mu_n/n\overset{P}{\longrightarrow} p$。

注意到 $\mu_n=\displaystyle\sum_{i=0}^nX_i$，令 $Y_n=\mu_n/n$，则 $E(Y_n)=p$，由切比雪夫大数定律知伯努利大数定律成立。

theorem 3（辛钦大数定律）：设 $X_1,X_2,\dots,X_n$ 是一列独立同分布的随机变量序列，且数学期望存在，即 $E(X_i)=\mu$，则 $\displaystyle\frac{1}{n}\sum_{i=1}^nX_i\overset{P}{\longrightarrow}\mu$。

定理三的证明要用到特征函数的知识，暂且不表。大数定律从定性的角度说明了样本均值以某种意义稳定于概率，而中心极限定理（central limit theorem）则告诉我们样本均值的分布情况。事实上，无论样本总体的分布如何，多次抽取的样本均值总会围绕在总体均值附近，并且呈正态分布。

theorem 4（中心极限定理）：设 $X_1,X_2,\dots,X_n$ 独立同分布，且 $E(X_i)=\mu$，$D(X_i)=\sigma^2$，则当 $n\rightarrow\infty$ 时，$\displaystyle\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1)$。

记 $S=\displaystyle\sum_{i=1}^nX_i$，$\bar{X}=\displaystyle\frac{1}{n}S$，$Y=\displaystyle\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}$，基于特征函数的性质我们可以得到：

\[\Phi_S(\omega)=\Phi_X^n(\omega)\qquad \Phi_{\bar{X}}(\omega)=\Phi_S(\frac{\omega}{n})=\Phi_X^n(\frac{\omega}{n})\] \[\Phi_Y(\omega)=e^{j(-\sqrt{n}/\sigma)\mu\omega}\cdot\Phi_{\bar{X}}(\frac{\sqrt{n}\omega}{\sigma})=e^{j(-\sqrt{n}/\sigma)\mu\omega}\cdot\Phi_X^n(\frac{\omega}{\sigma\sqrt{n}})\] \[\ln\Phi_Y(\omega)=\frac{-j\mu\frac{\omega}{\sigma\sqrt{n}}+\ln\Phi_X(\frac{\omega}{\sigma\sqrt{n}})}{1/n}\]

令 $p=\displaystyle\frac{\omega}{\sigma\sqrt{n}}$，注意 $\Phi_X(\omega)$ 在原点处的各阶导数值即 $X$ 各阶矩，对上式取极限我们有：

\[\lim_{n\rightarrow\infty}\ln\Phi_Y(\omega)=\frac{\omega^2}{\sigma^2}\lim_{p\rightarrow0}\frac{-j\mu p+\ln\Phi_X(p)}{p^2}=-\frac{\omega^2}{2}\]

因此 $\Phi_Y(\omega)=e^{-\omega^2/2}$，由特征函数的唯一性知 $Y\sim N(0,1)$。