逻辑（logic）

逻辑基础

逻辑是一切数学推理的基础，逻辑规则给出了数学语句的规范性描述（specification）。引入逻辑的根本目的在于能够将一般性问题转换为由连接词/运算符和简单命题（primitive）构筑成的复杂命题（proposition），并借助计算机实现快速求解。

\[\text{If you don't }\underbrace{\text{study hard}}\text{ , you will not }\underbrace{\text{get good grades}}\text{ .}\] \[\begin{cases} \text{study hard}=p \\ \text{get good grades}=q \end{cases}\Rightarrow \neg p\rightarrow\neg q\Leftrightarrow q\rightarrow p\Leftrightarrow p\vee\neg q\]

数学证明的一个重要步骤即用真值相同的一条语句替换另一条语句，因此真值永远为真/假的永真式（tautology）和矛盾式（contradiction）在证明中十分重要。实践中真值表（truth table）和逻辑等价式的替换可以帮助我们处理绝大多数的命题证明。

此外，为使简单命题具有一定的操作属性和明确的作用域（domain），我们引入了谓词（predicate）和量词（quantifier）来扩充逻辑语句可以精确表述的问题范围。

\[\exists x\forall y(x+y=y+x)\]

对于更为复杂的复合命题，我们常会结合逻辑等价式使用有效推理（valid inference）完成命题逻辑的有效论证（argument），例如著名的假言推理 $(p\wedge(p\rightarrow q))\rightarrow q$ 和假言三段论 $((p\rightarrow q)\wedge(q\rightarrow r))\rightarrow(p\rightarrow r)$。

在脱离计算机的具体实践中，我们往往会更加青睐富有智慧性的直接证明和构造性证明，亦或是剑走偏锋的反证法（proof by contraposition）。而基于递归结构和最小元思想的数学归纳法在计算机相关命题的证明上起着至关重要的作用。

良序原理（well-ordering principle）

良序原理的一般性表述为：$\mathbb{Z}^+$ 的任何非空子集均存在最小元素。自我指涉、归纳、递归均涉及结构的封闭性和最小元问题，派生自实数公理的良序原理为所有基于递归的结构性证明提供了逻辑基础。

数学归纳法（mathematical induction）

以多米诺骨牌为例，第一数学归纳法的通俗表述是：已知第一块会倒下；假设第 $k$ 块会倒下，那么第 $k+1$ 块也会倒下，这可以推出所有的骨牌都会倒下。第一数学归纳法的逻辑基点在于 $P(1)$，借助良序原理可以轻松证明第一数归的合理性。

\[(P(1)\wedge\forall k(P(k)\rightarrow P(k+1)))\rightarrow\forall nP(n)\]

馅饼攻击问题 $P(n)$：$2n+1$ 个人互相用馅饼攻击离自己最近的人，至少存在一个安全位置（以最短距离为边权，含奇数结点的有向图必然存在源）。

基础步骤：$P(1)$ 显然
归纳步骤：假设 $\forall k\geq1$，$P(k)$ 为真，对于 $P(k+1)$，考虑人群中距离最近的两人 $A,B$，则两人必相互攻击，那么：
- 其他人攻击 $A$ 或 $B$，则至少有 $3$ 张饼攻击了 $A,B$，而剩余的 $2k$ 张饼不可能涵盖 $A,B$ 外的 $2k+1$ 个人，因此必然存在安全位置
- 没有其他人攻击 $A,B$，由 $P(k)$ 知剩余的 $2k+1$ 人里存在安全位置
综上，$\forall n\in\mathbb{Z}^+P(n)$

第二数学归纳法/强归纳法（strong induction）

再以多米诺骨牌为例，第二数学归纳法的通俗表述是：已知第一块会倒下；假设前 $k$ 块会倒下，那么第 $k+1$ 块也会倒下，这可以推出所有的骨牌都会倒下。

\[(P(1)\wedge\forall k(P(1)\wedge P(2)\wedge\dots\wedge P(k)\rightarrow P(k+1)))\rightarrow\forall nP(n)\]

证明 $P(n)$：若 $n$ 是大于 $1$ 的整数，则 $n$ 可以写为素数之积。

基础步骤：$P(2)$ 显然
归纳步骤：假设 $\forall t\in[2,k]$，$P(t)$ 为真，我们有：
- $k+1$ 是素数，$P(k+1)$ 为真
- $k+1$ 非素数，记 $k+1=ab$，显然 $2\leq a,b\leq k$，此时 $P(a),P(b)$ 为真，$P(k+1)$ 为真

与第一数学归纳法相比，第二数学归纳法运用了更多的假设前件（前者只依赖于 $P(k)$），因此第二数学归纳法拥有更广泛的适用空间，在计算几何学、贪心算法可行性的证明上大有作用。事实上，良序原理、第一数学归纳法、第二数学归纳法三者是等价的。

离散结构（discrete structure）

集合（set）

集合是元素（element）的无序聚集，如整数集 $\mathbb{Z}$ 和自然数集 $\mathbb{N}$，通常我们用大写字母来表示集合，用小写字母表示集合中的元素。

\[A=\{0, 1, 2, 3, 4, 5\}\] \[B=\{x:x=2k+1,k\in\mathbb{N}\}\]

我们记 $\vert A\vert=6$ 为集合的基数（cardinality），用以表征集合的大小；记 $\mathbb{P}(A)$ 为集合 $A$ 的幂集，即 $A$ 所有子集的合集，显然 $\mathbb{P}(A)=2^{\vert A\vert}$。集合间运算可用文氏图（venn diagram）直观表示，如：

\[\vert A\cup B\vert=\vert A\vert+\vert B\vert-\vert A\cap B\vert\]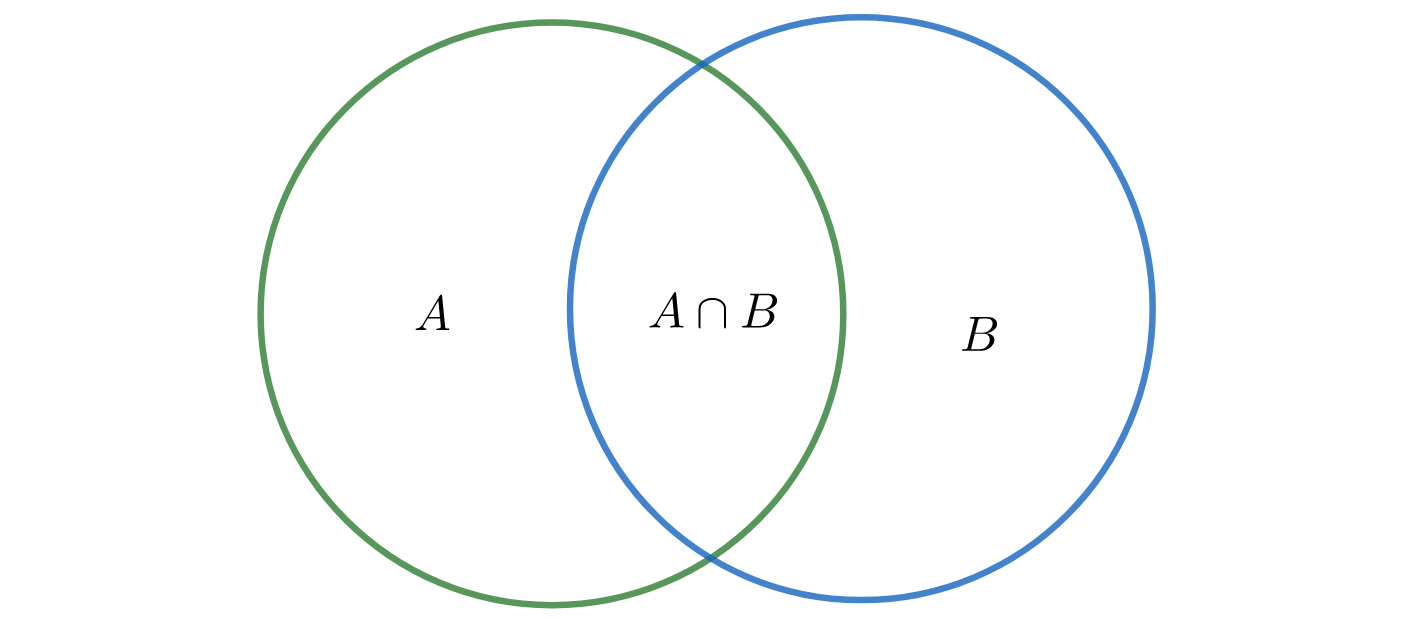

对于无限集，我们通过构造一对一映射来比较集合间的基数大小（实践中经常会构造两次单射结合伯恩斯坦定理证明集合基数相等），如 $\vert B\vert=\vert\mathbb{N}\vert$。我们称基数小于等于自然数集的集合为可列集（countable set），可列个可列集之并也是可列集。自然数集的势（基数）被记为 $\aleph_0$，事实上自然数集之上还存在基数更大的集合。可以证明，自然数幂集和实数集是等势的，即 $\vert\mathbb{P}(\mathbb{N})\vert=\vert\mathbb{R}\vert=\aleph_1$。
（Hint：$\vert\mathbb{P}(\mathbb{N})\vert=\vert\mathbb{R}\vert=\vert(0,1]\vert$，利用二进制小数构造双射）

关于序列/列表（sequence/list）、树（tree）和图（diagram），我们在数据结构中进行了翔实地阐述，这里不做赘述。

关系（relation）

为进一步了解集合内部元素间的关系，我们定义了集合上的笛卡尔积（Cartesian product）：

\[A\times B=\{(a,b):a\in A\wedge b\in B\}\]

显然 $\vert A\times B\vert=\vert A\vert\vert B\vert$。事实上，笛卡尔积严格给出了集合间有序对（pair）的定义，笛卡尔积的任何子集 $R$ 均可视作从集合 $A$ 到集合 $B$ 的一个关系（relation），一个从 $A$ 到 $B$ 的二元关系是 $A\times B$ 的子集，记作 $aRb$；集合 $A$ 上的关系是 $A\times A$ 的子集。

进一步，函数（function）定义了集合内或集合间元素到元素的映射关系，记为 $f:A\rightarrow B$。对于函数，我们需要额外关注的是它的定义域/原像（domain/preimage）和陪域（codomain/image），注意 $f$ 将定义域内的所有元素确定且唯一的映射至陪域上，因此函数是一类特殊的关系。

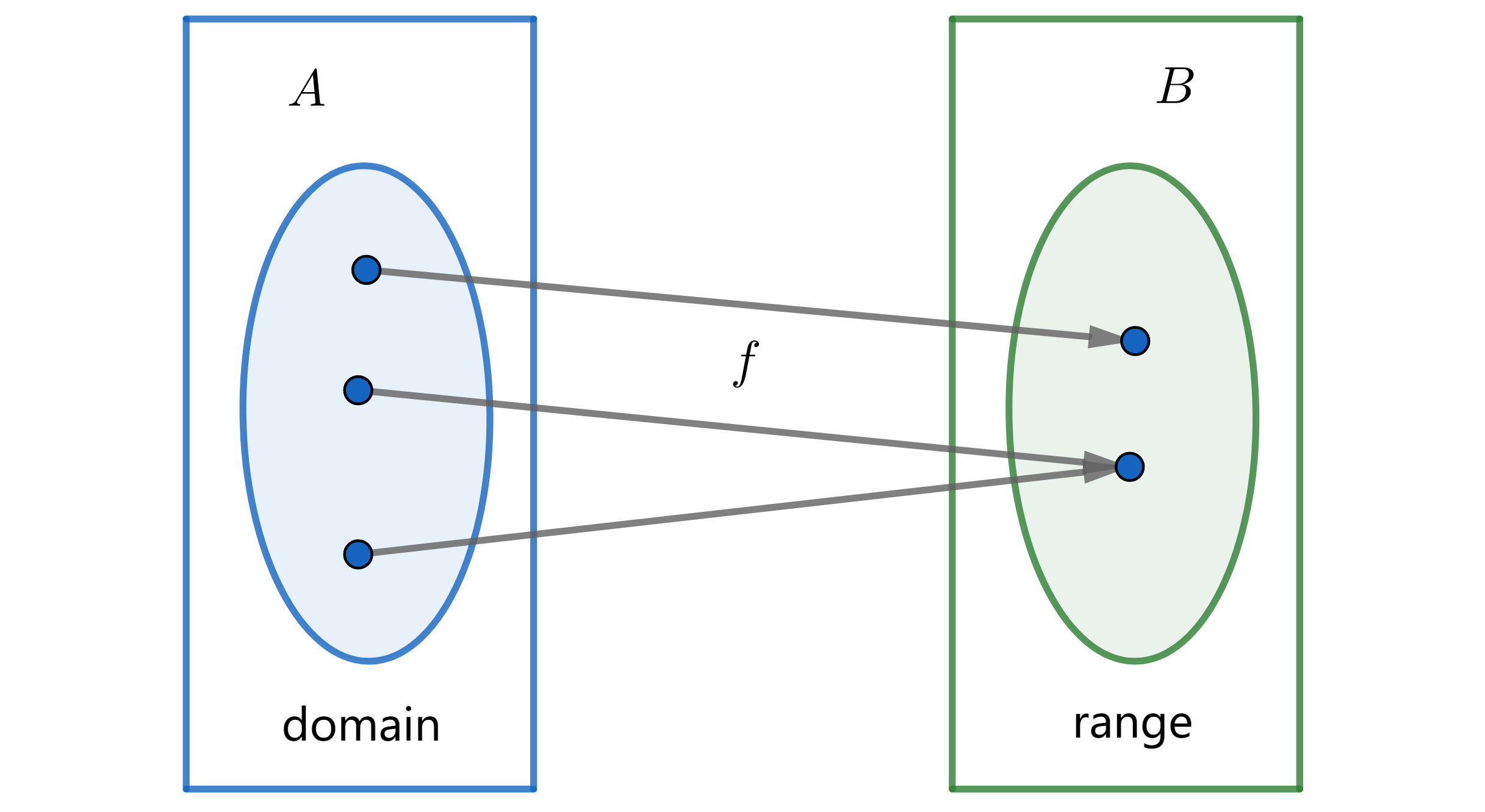
集合上关系有如下重要性质：

基本关系	表达式
自反（reflexive）	$\forall x\in A,(x,x)\in R$
对称（symmetric）	$\forall x,y\in A,(x,y)\in R\Rightarrow(y,x)\in R$
传递（transitive）	$\forall x,y,z\in A,(x,y),(y,z)\in R\Rightarrow (x,z)\in R$
反对称（antisymmetric）	$\forall x,y\in A,(aRb\wedge bRa)\Rightarrow a=b$

容易证明，$n$ 元集合上有 $2^{n^2}$ 个关系，$2^{n(n-1)}$ 个自反关系，$2^{n(n+1)/2}$ 个对称关系。关系作为一种特殊的离散结构也有类似于集合间的计算规则，以及与复合函数相仿的合成运算 $R\circ R=R^2$。

$n$ 元关系及其性质与关系型数据库的设计尤为密切，在此不做赘述。在具体的计算机实践中我们通常会格外关注二元关系及其表示形式，例如：

\[m_{ij}=\begin{cases} 1 & (a_i,b_j)\in R \\ 0 & (a_i,b_j)\notin R \end{cases}\Rightarrow M= \begin{bmatrix} 1 & 1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 1 \end{bmatrix}\]

容易看出，上述关系满足自反和对称性。使用矩阵（可由有向图代替）表示二元关系十分直观，同时关系的合成也很容易通过矩阵乘法快速得到。

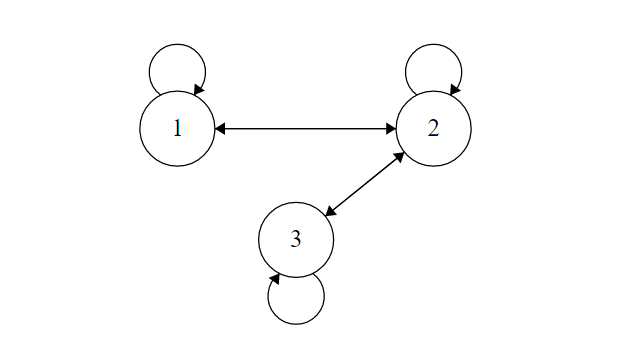
在图里我们可以看到二元关系反映的是局部两个相邻结点的关系，对于整体性质的刻画略显不足，因此我们引入了闭包（closure）的概念，用关系之外的结点间联系填充闭包。例如传递闭包就刻画了关系图的连通性（connectivity）：

\[M_T=M_R\vee M_{R^2}\vee\dots\vee M_{R^n}\]

$R$ 的幂体现了图中结点是否存在路径，上述朴素的算法其复杂度为 $O(n^4)$。沃舍尔算法（Warshall）提供了一个 $O(n^3)$ 计算传递闭包的思路：

procedure Warshall(M_T): // n x n
W := M_T
for k := 1 to n
    for i := 1 to n:
        for j := 1 to n:
        w_ij := w_ij | (w_ik & w_kj)
return W

Warshall 算法的构造思路和 Floyed 一致，内核是简单的遍历和迭代。对于给定的关系矩阵，经过 Warshall 的有限次迭代即可得到最终的传递闭包。

\[\begin{bmatrix} 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix}\Rightarrow\begin{bmatrix} 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 1 \end{bmatrix}\Rightarrow\begin{bmatrix} 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 \end{bmatrix}\Rightarrow\begin{bmatrix} 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 1 \end{bmatrix}\]

等价关系（equivalence relation）满足自反、对称、传递性。模 $m$ 同余关系是一个典型的等价关系。根据等价关系可以定义集合内某代表元素的等价类，如 $1$ 的模 $3$ 同余等价类 ${a:a\equiv1\pmod 3}$。根据等价类我们可以将集合划分为不相交的非空子集，显然模 $3$ 同余关系可以将整数集划分成 $3$ 个不相交子集。

\[\mathbb{Z}\Rightarrow\begin{cases} a\equiv0\pmod 3 \\ b\equiv1\pmod 3 \\ c\equiv2\pmod 3 \end{cases}\]

偏序关系（partial ordering relation）满足自反、反对称、传递性。$\geq$ 是整数集上的偏序，自然数集上的整除关系也是一个典型的偏序关系。若在集合 $A$ 上给定一个偏序关系 $\preccurlyeq$，则称 $(A,\preccurlyeq)$ 为偏序集；若偏序集内每对元素均有 $a\preccurlyeq b$ 或 $b\preccurlyeq a$，则该集为全序集（totally ordered set）或线序集（linearly ordered set）；若全序集 $A$ 的每个非空子集均有最小元素，则该集为良序集，良序集的定义是良序归纳的基础。

对于有穷偏序集，我们可以构造哈塞图（Hasse diagram）来观察其性质。哈塞图的构造算法十分简单：对于初始关系图，移除自身的环和传递产生的边，将边的起点置于终点下方即可。通过哈塞图可以轻松看出有穷偏序集内的极小元（位于底部）和极大元（位于顶部），下图示的哈塞图其极小元为 $1$，没有极大元。

如果一个偏序集的每对元素都有最小上界和最大下界，就称这个偏序集为格（lattice）。$(\mathbb{Z}^+,\vert)$ 是一个典型的格，集合内每对元素 $a,b$ 都有最小上界 $\text{lcm}(a,b)$ 和最大下界 $\gcd(a,b)$。严格基于安全和保密策略构筑成的信息流就可以用格模型来表示。

代数结构（algebraic structure）

代数结构是抽象代数研究的对象，代数主要研究的是运算规则，而一个集合再加上一套运算规则，就构成一个代数结构。对于代数结构，我们需要关注它的研究对象（指集合）、集合上的二元运算（binary operation）、运算是否满足结合律或交换律、集合是否存在幺元（identity element）和逆元（inverse element）。

一个简单的代数结构 $(S,*)$，根据二元运算满足的不同性质可以归纳为不同的群（group），例如 $(\mathbb{Z},+)$ 就是个典型的阿贝尔群/交换群（Abelian group）。

\[(S,*)\overset{封闭性}{\longrightarrow}\text{原群}\overset{结合律}{\longrightarrow}\text{半群}\overset{幺元}{\longrightarrow}\text{幺半群}\overset{逆元}{\longrightarrow}\text{群}\overset{交换律}{\longrightarrow}\text{阿贝尔群}\]

在交换群的基础上添加新的二元运算，在满足环公理（ring axioms）的前提下即可构成新的代数结构——环（ring）。对于环 $(S,+,\cdot)$，它满足：

$(S,+)$ 是交换群
$(S,\cdot)$ 是幺半群
$\cdot$ 对 $+$ 满足分配律：$a\cdot(b+c)=a\cdot b+a\cdot c$

若 $\cdot$ 也满足交换律，则该环可称为交换环（commutative ring）；若交换环内任意两非零元素 $\cdot$ 运算没有零因子，则该环升级为整环（integral domain），整环意味着 $a\not=0\wedge a\cdot b=a\cdot c\Rightarrow b=c$ 成立。

在交换环的基础上，如果环内任意非零元素均有乘法逆元，则该环升级为域（field）。域是数字与四则运算的推广，显然整数集不是域，而有理数、实数、复数均可形成域。

关于代数结构的研究到此为止，有兴趣的读者可进一步研读抽象代数等相关知识。

初等数论（primary number theory）

模算数（modular arithmetic）

\[\text{Dividend}\div\text{divisor}=\text{quotient}\dotsb\text{remainder}\] \[a\div b=q\dotsb r\Rightarrow a\bmod b=r\]

当 $r=0$，表示 $a$ 可被 $b$ 整除，记作 $b\mid a$，整数集上的整除关系是偏序关系，满足以下重要性质：

传递性：$a\mid b\wedge b\mid c\Rightarrow a\mid c$
线性：$a\mid b\wedge a\mid c\Rightarrow a\mid(bx+cy)\quad x,y\in\mathbb{Z}$

由模运算引申来的同余（congruence）关系定义为：$a\equiv b\pmod m\Leftrightarrow m\mid(a-b)$，容易证明加法和乘法是保同余的。

\[\begin{cases} a\equiv b\pmod m \\ c\equiv d\pmod m \end{cases}\Rightarrow \begin{cases} a+c\equiv b+d\pmod m \\ ac\equiv bd\pmod m \end{cases}\]

$\bmod$ 具备传染性，即外部的模运算可以传染至内部，常用于 ACM 中涉及大整数取模的运算，例如快速幂取模。传染性可借助同余式 $a\equiv(a\bmod m)\pmod m$ 轻松证明：

\[(a+b)\bmod m=[(a\bmod m)+(b\bmod m)]\bmod m\]

// 快速幂
int qpow(int x, int k){
    int res = 1;
    while(k){
        if(k & 1)
            res *= x;
        x *= x;
        k >>= 1;
    }
    return res;
}

// 快速幂取模
int qpow(int x, int k, int m){
    int res = 1;
    x %= m;
    while(k){
        if(k & 1)
            res = (res * x) % m;
        x = (x * x) % m;
        k >>= 1;
    }
    return res;
}

在有限整数集上我们可以定义模 $m$ 算术。容易证明，${\mathbb{Z}_m,+_m}$ 是一个交换群，${\mathbb{Z}_m,+_m,\cdot_m}$ 是一个交换环。

\[\mathbb{Z}_m=\{0,1,2,\dots,m-1\}\] \[a+_mb=(a+b)\bmod m\] \[a\cdot_mb=(a\cdot b)\bmod m\]

素数（prime）

算数基本定理（Fundamental Theorem of Arithmetic）

素数即除 $1$ 和自身外不含其它因子的数，算数基本定理告诉我们，任何大于 $1$ 的自然数均可表述为素因子之积，这意味着，我们可以以全体素数为基 $P={p_1,p_2,\dots,p_n}$ 表示自然数集（$1$ 为空集），任何自然数有且仅有一种非递减序素因子排列。

引理（lemma）：$p$ 是素数且 $p\mid a_1a_2\dots a_n$，则 $\exists a_i$，$p\mid a_i$
存在性证明：由第二数学归纳法易证
唯一性证明：假设 $n$ 有两种素因子排列，约去公共素因子后有 $p_1p_2\dots p_n=q_1q_2\dots q_m$，此时 $p_1\mid q_1q_2\dots q_m$，这与引理相矛盾，因此最多只有一种非递减序素因子排列

欧几里得定理说明存在无限多个素数，假设素数有限，记 $Q=p_1p_2\dots p_n+1$，根据整除的线性性质很容易推导出矛盾。也因此，素数的分布一直是数论中一个迷人的问题，素数定理告诉我们当 $x$ 无限增长时，$\pi(x)\sim1/\ln x$。关于定理的证明及其他更深入的研究，感兴趣的读者可以继续学习解析数论相关知识。

裴蜀定理/贝祖恒等式（Bézout’s identity）

素因子分解式还给出了两数最小公倍数（least common multiple）和最大公约数（greatest common divisor）的清晰定义：

\[a=p_1^{a_1}p_2^{a_2}\dots p_n^{a_n}\quad b=p_1^{b_1}p_2^{b_2}\dots p_n^{b_n}\] \[\gcd(a,b)=p_1^{\min(a_1,b_1)}p_2^{\min(a_2,b_2)}\dots p_n^{\min(a_n,b_n)}\] \[\text{lcm}(a,b)=p_1^{\max(a_1,b_1)}p_2^{\max(a_2,b_2)}\dots p_n^{\max(a_n,b_n)}\]

容易证明，$ab=\gcd(a,b)\times\text{lcm}(a,b)$，实践中我们通常使用欧几里得算法（辗转相除法）求两数的最大公约数。

\[\gcd(a,b)=\gcd(b,a\bmod b)\]

int gcd(int a, int b){
    while(b){
        a %= b;
        swap(a, b);
    }
    return a;
}

事实上，$\gcd$ 还可用两数的线性组合表示，即裴蜀定理（贝祖定理）。裴蜀定理的一般表述为，线性组合 $ax+by$ 一定是 $\gcd(a,b)$ 的倍数，特别的，$\exists x,y\in\mathbb{Z}$，$\gcd(a,b)=ax+by$。

记 $\gcd(a,b)=k$，显然 $k\mid(ax+by)$。设 $s$ 是 $ax+by$ 的最小元（非负），记 $q=a\div s$，则：

\[r=a\bmod s=a-qs=a(1-qx)+b(-qy)\]

可见 $r$ 也是 $a,b$ 的线性组合，$0\leq r<s$，因此 $r=0$，$s\mid a$，同理可证 $s\mid b$，因此 $s\mid k$，由整除的自反性知 $s=k$，裴蜀定理得证。

裴蜀定理的一个重要推论是：当 $a,b$ 互质，即 $\gcd(a,b)=1$，$\exists x,y\in\mathbb{Z}$，$ax+by=1$。利用裴蜀定理还可以轻松证明一些有趣的推论，如：

$a\mid bc\wedge\gcd(a,b)=1\Rightarrow a\mid c$
$a/\gcd(a,b)$ 和 $b/\gcd(a,b)$ 互质
$ac\equiv bc\pmod m\wedge\gcd(c,m)=1\Rightarrow a\equiv b\pmod m$
$ac\equiv bc\pmod m\Rightarrow a\equiv b\pmod{m/\gcd(c,m)}$

裴蜀定理的相关系数可借助扩展欧几里得算法（extended Euclidean algorithm）快速求解，其内核实质上是欧几里得算法的逆过程。

\[\begin{cases} ax_1+by_1=\gcd(a,b) \\ bx_2+(a\bmod b)y_2=\gcd(b,a\bmod b) \end{cases}\Rightarrow \gcd(a,b)\times1+0\times0=\gcd(a,b)\] \[ax_1+by_1=bx_2+(a\bmod b)y_2=ay_2+b(x_2-a\div b\times y_2)\] \[\Rightarrow\begin{cases} x_1=y_2 \\ y_1=x_2-a\div b\times y_2 \end{cases}\]

// 同时求最大公因数和裴蜀系数
int exgcd(int a, int b, int &x, int &y){
    if(b == 0){
        x = 1;
        y = 0;
        return a;
    }
    int r = exgcd(b, a % b, x, y);
    int tmp = x, x = y;
    y = t - a / b * y;
    return r;
}

借助迭代式即可快速求得裴蜀定理的相关系数，该算法亦适用于乘法逆元的快速求解。

同余方程（congruence）

线性同余方程一般形式为 $ax\equiv b\pmod m$，当 $a$ 具有乘法逆元时该方程的求解将变得十分简单（两边同乘逆元即可）。$a$ 模 $m$ 的乘法逆元 $x$ 满足 $ax\equiv1\pmod m$，容易证明 $a$ 具备乘法逆元的充要条件是 $a,m$ 互质，即有 $ax+my=1$。利用扩展欧几里得可以快速求出 $ax+my=1$ 的贝祖系数，进而得到 $a$ 的乘法逆元。

\[3x\equiv4(\bmod7)\Rightarrow3\times5\equiv1(\bmod7)\Rightarrow x\equiv20(\bmod7)\]

线性同余方程组也十分常见，当方程组的模数两两互质时，中国剩余定理（Chinese remainder theorem）给出了构造性的唯一解（其他解与之模 $m$ 同余）：

\[\begin{cases} x\equiv a_1\pmod {m_1} \\ x\equiv a_2\pmod {m_2} \\ \quad\cdots\cdots\\ x\equiv a_n\pmod {m_n} \end{cases}\]

记 $m=\prod m_i$，$M_k=m/m_k$，则 $\gcd(m_k,M_k)=1\Rightarrow M_ky_k\equiv1\pmod {m_k}$，因此：

\[x=a_1M_1y_1+a_2M_2y_2+\dots+a_nM_ny_n\]

该构造性证明是浅显易懂的，例如对于 $x\equiv a_1\pmod {m_1}$，$x$ 除首项均可被 $m_1$ 整除，而 $a_1M_1y_1\equiv a_1\pmod {m_1}$ 是显然的。利用中国剩余定理我们可以轻松解答孙子的问题：“有物不知其数，三分之余二，五分之余三，七分之余二，此物几何？”

\[\begin{cases} x\equiv 2\pmod 3 \\ x\equiv 3\pmod 5 \\ x\equiv 2\pmod 7 \end{cases}\Rightarrow x=233\equiv23\pmod {105}\]

lemma 1：$p$ 是素数，则 $x^2\equiv1\pmod p$ 仅有的解满足 $x\equiv1\pmod p$ 或 $x\equiv-1\pmod p$。

lemma 2：$p$ 是素数，则集合 ${x\in\mathbb{Z}:1<x<p-1}$ 可分割成一对对整数，每对整数互为模 $p$ 的逆。

对于引理 2，当 $p=2$ 或 $p=3$ 时显然，当 $p\geq5$ 时我们可以做以下构造性证明：

\[M=\{2,3,\dots,p-2\}\quad N=\{1,2,\dots,p-1\}\] \[\forall a\in M,\quad S=\{a,2a,\dots,(p-1)a\}\]

注意 $\forall t\in S$，$p\nmid t$，因此 $\forall t_1,t_2\in S$，$t_1<t_2$，有 $p\nmid(t_2-t_1)$。因此 $S$ 中任意两对数模 $p$ 不同余，且 $M$ 中任意元素若存在则仅存在唯一的小于 $p$ 的模 $p$ 逆元。事实上 $N$ 和 $S$ 均是模 $p$ 的一个完全剩余系（complete residue system，模 $p$ 同余等价类各取一个数）。因此 $S\bmod p=N$，即 $\forall a\in M\exists x\in N$，$ax\equiv1\pmod p$。

威尔逊定理（Wilson’s theorem）：$(p-1)!\equiv-1\pmod p$ 当且仅当 $p$ 是素数。

充分性：$(p-1)!\equiv p-1\equiv-1\pmod p$
必要性：假设 $p$ 是合数，即 $p=ab$，$1<a,b<p$，则 $a\mid (p-1)!$，而 $a\mid p\mid(p-1!)+1$，得出 $a\mid1$，即 $a=1$，这与 $a>1$ 矛盾，因此 $p$ 是素数

费马小定理（Fermat’s little theorem）：$\gcd(a,p)=1$，有 $a^{p-1}\equiv1\pmod p$。

由于 $\gcd(a,p)=1$，我们可以效仿引理 2 构造模 $p$ 的完全剩余系 $S$，因此 $a^{p-1}(p-1)!\equiv(p-1)!\pmod p$，又因为 $\gcd((p-1)!,p)=1$，所以 $a^{p-1}\equiv1\pmod p$ 成立。

威尔逊定理和费马小定理的证明均借助了完全剩余系的构造。对完全剩余系缩减可得到既约剩余系（reduced residue system），它是欧拉定理（Euler theorem）证明的关键。欧拉函数 $\phi(x)$ 表小于等于 $x$ 的正整数中与 $x$ 互质的个数，模 $n$ 的既约剩余系是由 $\phi(n)$ 个整数构成的集合，集合中的每个元素均与 $n$ 互质，且任何两个元素模 $n$ 不同余。

lemma 3：设 ${r_1,r_2,\dots,r_{\phi(n)}}$ 是模 $n$ 的一个既约剩余系，若正整数 $a$ 满足 $\gcd(a,n)=1$，那么 ${ar_1,ar_2,\dots,ar_{\phi(n)}}$ 也是一个既约剩余系。

借助既约剩余系我们很容易得到 $a^{\phi(n)}r_1r_2\dots r_{\phi(n)}\equiv r_1r_2\dots r_{\phi(n)}\pmod n$，由于 $\gcd(r_1r_2\dots r_{\phi(n)},n)=1$，因此 $a^{\phi(n)}\equiv1\pmod n$，欧拉定理得证。

以上，借助剩余系，威尔逊定理、费马小定理和欧拉定理给出了大数幂取模和求乘法逆元（如果存在）的新方法。关于定理的其他应用感兴趣的读者可以进一步学习解析数论相关知识。

RSA 密码系统（RSA cryptosystem）

利用同余关系我们可以设计一个优秀的密码系统，一个好的密码系统往往会公开加密方式，通过特定的解密密钥实现解锁。在 RSA 密码系统中，每个人都有一个加密密钥 $(n,e)$，其中 $n=pq$ 是两个大素数的乘积，$e$ 是与 $(p-1)(q-1)$ 互质的指数。

\[C=M^e\bmod n\]

RSA 密码系统的解密密钥 $d$ 是 $e$ 模 $(p-1)(q-1)$ 的逆，即 $de\equiv1\pmod{(p-1)(q-1)}$。当已知解密密钥时，对密文的解密将变得十分简单：

\[C^d\equiv M^{ed}\equiv M^{1+k(p-1)(q-1)}\pmod n\] \[\begin{cases} C^d\equiv M(M^{p-1})^{k(q-1)}\equiv M\pmod p \\ C^d\equiv M(M^{q-1})^{k(p-1)}\equiv M\pmod q \end{cases}\Rightarrow M\equiv C^d\pmod{pq}\]

根据 CRT 我们能快速得出 $M\equiv C^d\pmod n$。注意上述证明做了 $\gcd(M,p)=\gcd(M,q)=1$ 的假设，事实上这一关系只有在极罕见的情况下不成立。RSA 之所以是优秀的密码系统，是因为我们可以快速找到大素数 $p,q$ 和指数 $e$ 构造一个公钥，借助扩展欧几里得计算出解密密钥 $d$。而对于不知道解密密钥的人来说，对 $n$ 这种大整数进行因式分解目前是不可能在合理时间内完成的。

计数（count）

排列组合（permutation and combination）

计数是组合数学的重要部分，基本的计数原则即求和原则（rule of sum）和乘法原则（rule of product）。而排列和组合永远是计数的核心问题。以下公式给出了从 $n$ 个物品选 $r$ 个物品排列和组合的种数：

\[P(n,r)=\frac{n!}{(n-r)!}\] \[C(n,r)=\frac{n!}{r!(n-r)!}=\binom{n}{r}=\binom{n}{n-r}\]

场景 1：可重全排列，$n$ 个元素形成了 $r$ 个聚类 $n_1+n_2+\dots+n_r=n$，计算元素的全排列时就要考虑聚类内部元素相同的问题，此时：

\[P=\frac{n!}{n_1!n_2!\dots n_r!}\]

例：路径问题，一个 $6\times3$ 的网格盘，从左上角走到右上角有多少种路径？

\[P=\frac{9!}{6!\times3!}=84\]

场景 2：圆排列，$n$ 个人在圆桌上排座，由于每个人都可以成为起点，故圆排列的公式即 $n!/n$。

场景 3：可重复组合，即允许元素重复的组合数，从 $n$ 类不同物品中组合 $r$ 个，等价于将 $r$ 的相同物品扔进 $n$ 个不同坑的种数，等价于下述不定方程解的个数，用隔板法可以轻松得出计算公式：

\[x_1+x_2+\dots+x_n=r\quad x_i\in\mathbb{N}\] \[y_1+y_2+\dots+y_n=n+r\quad y_i\in\mathbb{N}^+\] \[C=\binom{n+r-1}{n-1}=\binom{n+r-1}{r}\]

例：三个糖分给四个小朋友：$\binom{4+3-1}{3}$；七个人住进四家宾馆：$\binom{4+7-1}{7}$

在组合数学中我们常会使用组合证明（combinatorial proof）的方式，构造场景利用排列组合证明一些组合恒等式，例如二项式定理（binomial theorem）：

\[(x+y)^n=\binom{n}{0}x^0y^n+\binom{n}{1}x^1y^{n-1}+\dots+\binom{n}{n}x^ny^0\]

数的合成问题，即对于正整数 $n$，有 $2^{n-1}$ 种加和组合方式（例如 $4=2+2$，$4=1+2+1$），利用隔板法可以轻松证明。

\[n\Rightarrow\sum_{k=0}^{n-1}\binom{n-1}{k}=2^{n-1}\]

帕斯卡恒等式（Pascal’s identity），帕斯卡三角（杨辉三角）中一个数等于其肩上两数之和，构造性证明如下：

\[\binom{n+1}{k}=\binom{n}{k-1}+\binom{n}{k}\]

定义集合 $S$ 满足 $\vert S\vert=n+1$，从 $S$ 中选一个大小为 $k$ 的子集，有 $\binom{n+1}{k}$ 种可能。对于某特定元素 $a\in S$，子集包含 $a$ 的可能有 $\binom{n}{k-1}$ 种，不含 $a$ 的可能有 $\binom{n}{k}$ 种。

卡特兰数（catalan）描述了合法排列可能的种数。对于长为 $2n$ 的二进制串，它的合法排列满足：

$0$ 的数目等于 $1$ 的数目
以首字符开始的任意子串均有 $0$ 的数目大于等于 $1$ 的数目（如 $0101$，$0011$）

现在我们来计算合法排列的种数，首先在 $2n$ 个位置放 $n$ 个 $0$ 有 $\binom{2n}{n}$ 种可能，然后我们考虑所有错误排列的情形。对于每一种错误排列，必然能找到一个位置，使得首字符到该位置组成的串 $1$ 比 $0$ 刚好多一个：

\[\underbrace{00111}\dots0101001\]

此时前串和后串无论怎么变换排列都不可能生成一个正确的串。对前串取反（这不改变排列的种数），则错误的串等价于 $n+1$ 个 $0$ 和 $n-1$ 个 1 组合成的串，有 $\binom{2n}{n+1}$ 种可能，所以：

\[\binom{2n}{n}-\binom{2n}{n+1}=\frac{1}{n+1}\binom{2n}{n}\]

以上即卡特兰数的表达式，诸如合法括号序列、正确的出栈序列种数均与卡特兰数有关。

容斥原理（the principle of inclusion-exclusion）

设集合 $S$ 满足 $\vert S\vert=N$，条件组 ${c_1,c_2,\dots,c_t}$，记 $N(c_i)$ 是集合中满足条件 $c_i$ 的元素数目，$A_i$ 是满足条件 $c_i$ 的元素集合，则：

\[N(c_1c_2\dots c_t)=\vert A_1\cap A_2\cap\dots\cap A_t\vert\] \[N(\bar{c_1}\bar{c_2}\dots\bar{c_t})=N-\vert A_1\cup A_2\cup\dots\cup A_t\vert\] \[N(\bar{c_1}\bar{c_2}\dots\bar{c_t})=N-\sum_{1\leq i\leq t}N(c_i)+\sum_{1\leq i<j\leq t}N(c_ic_j)-\dots+(-1)^tN(c_1c_2\dots c_t)\]

考虑 $S$ 中任意一个满足 $r$ 个条件的元素 $x$，下列等式说明了对于每一个 $x\in S$，$x$ 计算且仅被计算了一次，因此容斥原理是成立的。

\[1=\binom{r}{1}-\binom{r}{2}+\dots+(-1)^r\binom{r}{r}\]

容斥原理的集合等价形式如下，其中 $A_i$ 为有穷集，当 $t$ 比较小时我们可以在 Venn 图上直观的看出这种计数方式的原理。

\[\vert A_1\cup A_2\cup\dots\cup A_t\vert=\sum_{1\leq i\leq t}\vert A_i\vert+\sum_{1\leq i<j\leq t}\vert A_i\cap A_j\vert-\dots+(-1)^t\vert A_1\cap A_2\cap\dots\cap A_t\vert\]

例 1：考虑带限不定方程 $x_1+x_2=8$，其中 $0\leq x_i\leq 5$，记 $c_i$ 表 $x_i>5$，我们就可以用容斥原理得出该带限不定方程解的组数为 $3$。

\[N=\binom{8+2-1}{8}=9\quad N(c_1c_2)=0\] \[N(c_1)=N(c_2)=\binom{2+2-1}{2}=3\] \[N(\bar{c_1}\bar{c_2})=N-N(c_1)-N(c_2)+N(c_1c_2)=9-6=3\]

例 2：证明 $\phi(p)=p-1$，其中 $\phi(n)$ 是欧拉函数，$p$ 是素数。

设 $n=p_1^{e_1}p_2^{e_2}\dots p_t^{e_t}$，记 $c_i$ 表 $p_i\mid n$，则：

\[\phi(n)=N(\bar{c_1}\bar{c_2}\dots\bar{c_t})=n-\sum_{1\leq i\leq t}\frac{n}{p_i}+\sum_{1\leq i<j\leq t}\frac{n}{p_ip_j}-\dots+(-1)^t\frac{n}{p_1p_2\dots p_t}=n\prod_{p\mid n}(1-\frac{1}{p})\]

当 $p$ 是素数时显然有 $\phi(p)=p(1-\displaystyle\frac{1}{p})=p-1$。

例 3：全错位排列（derangement），即没有一个元素在它正确的位置上（例如 $23451$），求 $n$ 元素集合的错位排列数。

记 $c_i$ 表第 $i$ 个元素在它正确的位置上，则错位排列数即 $N(\bar{c_1}\bar{c_2}\dots\bar{c_n})$。注意到 $N=n!$，$N(c_i)=(n-1)!$（第 $i$ 个位置确定，其他位置随意），类似的 $N(\bar{c_1}\bar{c_2}\dots\bar{c_m})=(n-m)!$，因此：

\[\begin{aligned} N(\bar{c_1}\bar{c_2}\dots\bar{c_n}) &= n!-\binom{n}{1}(n-1)!+\binom{n}{2}(n-2)!-\dots+(-1)^n\binom{n}{n}(n-n)! \\ &= n!(1-\frac{1}{1!}+\frac{1}{2!}-\dots+(-1)^n\frac{1}{n!}) \end{aligned}\]

容易证明，当 $n$ 趋向无穷时全错位排列发生的概率趋于 $e^{-1}$。

鸽巢原理（pigeonhole principle）

有 $m$ 只鸽子飞往 $n$ 个鸽巢栖息（$m>n$），则至少有一个鸽巢里栖息着 $\lceil m/n \rceil$ 只鸽子，这就是鸽巢原理的一般表述。鸽巢原理虽然描述简单，但其在很多问题上都有不俗的表现。

例 1：证明 $S={1,2,\dots,9}$ 大小为 $6$ 的任意子集必有两个和为 $10$ 的数。

\[S\Rightarrow\{1,9\},\{2,8\},\{3,7\},\{4,6\},\{5\}\]

对 $S$ 做以上划分，由鸽巢原理知 $S$ 大小为 $6$ 的子集中必然存在两个元素同时落入上述划分的某个集合里，故原命题得证。

例 2：已知 $m\in\mathbb{Z}^+$，且 $m$ 是奇数，证明 $\exists n\in\mathbb{Z}^+$，$m\mid2^n-1$。

\[S=\{2^1-1,2^2-1,\dots,2^{m+1}-1\}\]

模 $m$ 的完全剩余系大小为 $m$，考虑集合 $S$，由鸽巢原理知 $\exists s,t\in\mathbb{Z}^+$，$1\leq s<t\leq t\leq m+1$，$2^s-1\equiv2^t-1\pmod m$，所以 $m\mid2^s(2^{t-s}-1)$，而 $\gcd(2^s,m)=1$，所以 $m\mid2^{t-s}-1$，原命题得证。

生成函数（generating function）

中学阶段我们多用递推式来表示序列（$a_{n+1}=2a_n+1$），结合不动点、迭代函数和特征方程三大利器可以轻松解出递推式的解析式。表示序列的另一种有效方法就是生成函数，它把序列的项表示为幂级数中 $x$ 的系数，利用级数的运算性质简化了序列计算问题。

\[G(x)=a_0+a_1x+a_2x^2+\dots+a_kx^k\]

例如求带限不定方程解的组数时，利用生成函数可以直观看出特定情形的解的组数。

\[x_1+x_2+x_3=17\quad(2\leq x_1,x_2\leq 5,4\leq x_3\leq7)\] \[G(x)=(x^2+x^3+x^4+x^5)^2(x^4+x^5+x^6+x^7)\]

展开 $G(x)$，$x^{17}$ 的系数即该带限不定方程的解的组数。注意这种计算方式和枚举并无二致，只是为读者提供了一种更加直观的视角，也方便计算机代数系统做这种计算。

下面我们将使用生成函数来处理一些有趣的问题，在这之前我们需要在指数不是正整数的情况下应用二项式定理，所以我们首先定义广义二项式系数：

\[\binom{u}{k}=\begin{cases} u(u-1)\dots(u-k+1)/k! & k>0 \\ 1 & k=0 \end{cases}\]

设 $x,u\in\mathbb{R}$ 且 $\vert x\vert<1$，对 $(1+x)^u$ 作麦克劳林展开即可证明广义二项式定理：

\[(1+x)^u=\sum_{k=0}^{\infty}\binom{u}{k}x^k\]

例 1：可重复组合问题（从 $n$ 类不同物品中组合 $r$ 个），我们可以写出以 $a_r$ 为序列的生成函数：

\[G(x)=(1+x+x^2+\dots)^n=(1-x)^{-n}=\sum_{r=0}^{\infty}\binom{-n}{r}(-x)^r\] \[\binom{-n}{r}(-1)^r=\binom{n+r-1}{r}\]

因此可重复组合问题的解即 $x^r$ 的系数，这与我们使用隔板法得出的结论一致。

例 2：从 $n$ 类不同物品中组合 $r$ 个，且每类物体至少选一个（$r\geq n$），我们同样可以写出以 $a_r$ 为序列的生成函数：

\[\begin{aligned} G(x) &= (x+x^2+\dots)^n=x^n(1-x)^{-n} \\ &= x^n\sum_{r=0}^{\infty}\binom{-n}{r}(-x)^r \\ &= \sum_{r=0}^{\infty}\binom{n+r-1}{r}x^{n+r} \\ &= \sum_{t=n}^{\infty}\binom{t-1}{t-n}x^t \end{aligned}\]

因此至少选一个的可重复组合问题的解即 $x^r$ 的系数 $\binom{r-1}{r-n}$。

例 3：已知 $a_n=8a_{n-1}+10^{n-1}$，$a_1=9$，$a_0=1$，求 $a_n$ 的表达式。

\[\begin{aligned} a_nx^n &= 8a_{n-1}x^n+10^{n-1}x^n \\ G(x)-1 &= 8xG(x)+\frac{x}{1-10x}\quad(\text{累加}) \end{aligned}\] \[G(x)=\frac{1}{2}(\frac{1}{1-8x}+\frac{1}{1-10x})=\sum_{n=0}^\infty\frac{1}{2}(8^n+10^n)x^n\] \[a_n=\frac{1}{2}(8^n+10^n)\]

例 4：证明 $\displaystyle\sum_{k=0}^n\binom{n}{k}^2=\binom{2n}{n}$，注意右部是 $(1+x)^{2n}$ 展开式 $x^n$ 的系数。

\[[(1+x)^n]^2=[\binom{n}{0}+\binom{n}{1}x+\dots+\binom{n}{n}x^n]^2\] \[x^n:\binom{n}{0}\binom{n}{n}+\binom{n}{1}\binom{n}{n-1}+\dots+\binom{n}{n}\binom{n}{0}=\sum_{k=0}^n\binom{n}{k}^2\]

以上，生成函数其内核是通过幂级数直观的展示枚举过程，幂级数简洁的运算性质赋予了生成函数在计数上的魅力。