矩阵(matrix)
向量空间(vector space)
向量(vector)是标量的有序组合,如位置向量 $\pmb{x}=[2,3,5]^T$。向量与欧氏空间内的点(point)一一对应,其丰富的几何性质赋予了向量简洁的运算规则,这就是引入向量的根本原因。在欧式空间的视角下,向量可以看作是多个基底(basis)的加权组合,我们可以用左乘矩阵来表述这种关系:
\[\begin{bmatrix} 3 \\ 2 \end{bmatrix} =3 \begin{bmatrix} 1 \\ 0 \end{bmatrix} +2 \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 3 \\ 2 \end{bmatrix}\]考虑向量 $\pmb{b}_1=[1,0]^T$,$\pmb{b}_2=[1,1]^T$ ,以 $B=[\pmb{b}_1, \pmb{b}_2]$ 为新基底,很容易得出原始坐标 $(3,2)$ 在新基下的坐标为 $(1,2)$。事实上这种对应关系亦可以扩展至整个 $\mathbb{R}^2$ 平面。
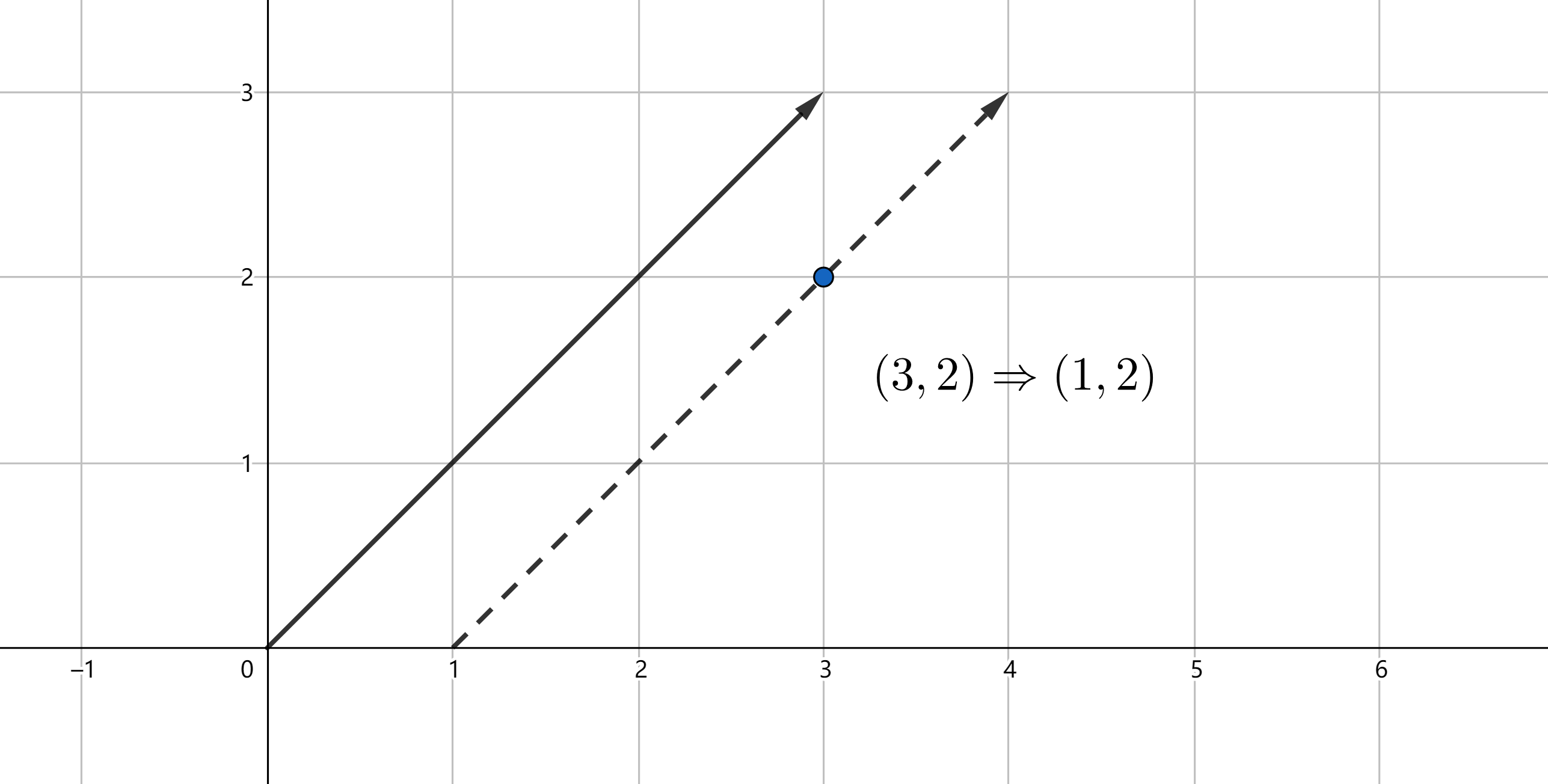
可以看出,欧式空间下的同一点,在不同基的表示下会得出不同的坐标,据此我们可以得出欧氏空间内的坐标变换公式: $\pmb{x}=P_B\pmb{x}_B$。同时我们也揭示了左乘矩阵的本质,即换基,显式的建立欧氏空间内不同基表示的点的坐标间的映射关系。在计算机图形学领域内,我们能更加直观的理解矩阵所表示的这种映射关系,如剪切变换(shearing)、旋转变换(rotation)等。
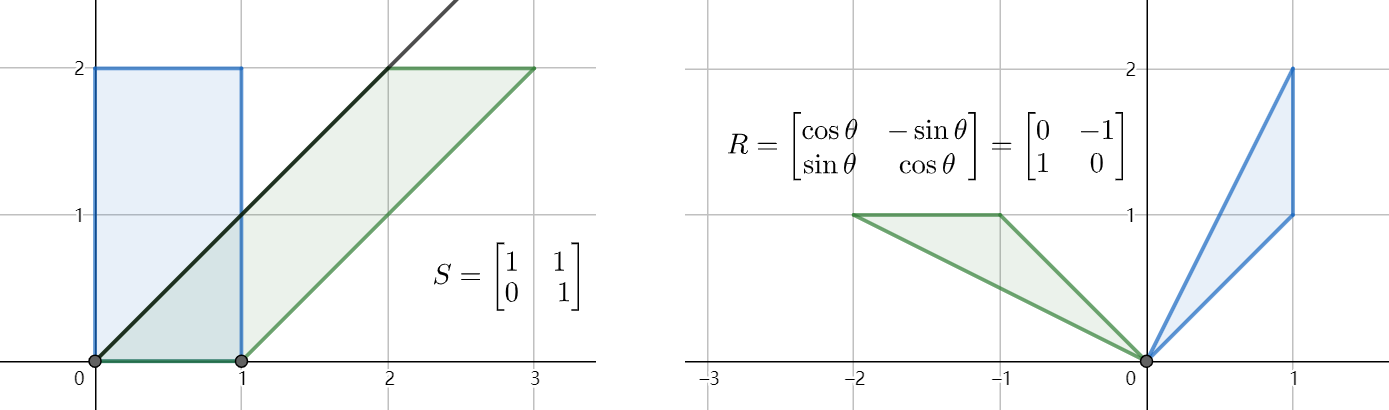
考虑变换 $T(\pmb{x})=A_{m\times n}\pmb{x}$,该变换以 $A$ 的列向量为基底建立了 $\mathbb{R}^n\rightarrow\mathbb{R}^m$ 的映射关系,$\mathbb{R}^n$ 和 $\mathbb{R}^m$ 被称为向量空间(线性空间)。这种变换与函数类似,均具有线性($f+g$)和可复合性($f\circ g$),这也是矩阵加法和乘法的意义所在。因此矩阵,其实质就是向量空间上的线性变换。
内积(dot product)
为了更好的度量向量的几何性质,我们引入了内积(dot product)的概念。考虑 $\mathbb{R}^n$ 中的向量 $\pmb{a}$ 和 $\pmb{b}$,它们的内积被简单定义为:$\langle\pmb{a},\pmb{b}\rangle=\pmb{a}\cdot\pmb{b}=\pmb{b}^T\pmb{a}$。内积可表述的相关几何性质如下表所示:
| 内积表示 | 几何含义 |
|---|---|
| $\parallel\pmb{a}\parallel=\pmb{a}\cdot\pmb{a}$ | 向量长度的平方 |
| $\pmb{a}\cdot\pmb{b}=0$ | 向量垂直(正交) |
| $\cos\theta=\displaystyle\frac{\pmb{a}\cdot\pmb{b}}{\parallel\pmb{a}\parallel\parallel\pmb{b}\parallel}$ | 向量间夹角 |
进一步,我们将向量空间 $V$ 与 $W$ 的正交性解释为:$V$ 内的任意向量与 $W$ 内的任意向量内积均为零,此时 $W$ 可称为 $V$ 的正交补空间,记作 $V^\bot$。
以上属于向量空间内的内积,在不同基的视角下内积亦可推广至其他空间,例如函数空间内的内积 $\langle f,g\rangle=\int_a^bf(t)g(t)\rm{d}t$,多项式空间内基于内积生成的正交多项式等。
线性方程组(linear equations)
本科阶段的学习大多从线性方程组的解来引出矩阵乘法的定义,从解析式上看线性方程组的解与矩阵方程的解无疑是等价的。
\[\begin{cases} x-2z=1 \\ x+2y=5 \\ y+z=2 \end{cases} \iff \begin{bmatrix} 1 & 0 & -2 \\ 1 & 2 & 5 \\ 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 1 \\ 5 \\ 2 \end{bmatrix}\]考虑右侧的矩阵方程 $A\pmb{x}=\pmb{b}$,它表示以 $A$ 的列向量为基底对 $\pmb{x}$ 进行线性变换得到 $\pmb{b}$。记 $A=[\pmb{c}_1,\pmb{c}_2]$,为方便表述我们称由矩阵列向量张成的子空间为列空间(column space),即满足 $\pmb{y}=A\pmb{x}$ 的 $\pmb{y}$ 的集合。方程可解即表示为 $b\in\text{span}(\pmb{c_1},\pmb{c_2})$,即 $\pmb{b}\in C(A)$。方程的解可以通过高斯消元法对增广矩阵(augmented bmatrix)进行初等行变换得到:
\[\left[\begin{array}{ccc|c} 1 & 0 & -2 & 1\\ 1 & 2 & 5 & 5\\ 0 & 1 & 1 & 2\\ \end{array}\right]\rightarrow \left[\begin{array}{ccc|c} 1 & 0 & -2 & 1\\ 0 & 1 & 1 & 2\\ 0 & 0 & 0 & 0\\ \end{array}\right]\] \[\pmb{x}= \begin{bmatrix} 1 \\ 2 \\ 0 \end{bmatrix}+ k\begin{bmatrix} 2 \\ -1 \\ 0 \end{bmatrix},k\in\mathbb{R}\]再考虑齐次方程 $A\pmb{x}=\pmb{0}$,显然行变换不会影响等式右侧的零,最终得到的解为 $\pmb{x}=[2k,-k,0]^T$,与 $A\pmb{x}=\pmb{b}$ 的解集相比仅仅差了一个常向量(constant vector)。我们称所有满足 $A\pmb{x}=\pmb{0}$ 的 $\pmb{x}$ 的集合为 $A$ 的零空间(null space),$A\pmb{x}=\pmb{b}$ 的解空间可看作是零空间的整体平移,两个空间存在一个恒等的偏差(bias)。
对于 $A$ 进行初等行变换得到的上三角矩阵 $U_{m\times n}$,称对角线上的非零元为主元(pivot),称零元为自由变量(free variables),我们很容易就能找到一个关于秩和零空间的著名定理:秩-零度定理(rank-nullity theorem)
\[\text{rank}A+N(A)=\#\text{pivot}+\#\text{free variables}=m\]以上,我们通过线性方程组引入了矩阵的两个重要性质:列空间与零空间。将 $A$ 改写为 $[r_1,r_2,r_3]^T$,对转置后的矩阵引入行空间(row space)与左零空间(column space of A transpose)的概念,敏锐的读者很快就能发现,矩阵的行空间与零空间事实上是正交的(orthogonal)。
\[A\pmb{x}=\pmb{0}\rightarrow \begin{bmatrix} \pmb{r}_1 \\ \pmb{r}_2 \\ \pmb{r}_3 \end{bmatrix}\pmb{x}= \begin{bmatrix} \pmb{r}_1\cdot\pmb{x} \\ \pmb{r}_2\cdot\pmb{x} \\ \pmb{r}_3\cdot\pmb{x} \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}\]由于行空间与零空间的正交互补性,结合秩-零度定理,我们可以得到关于秩的一个经典结论:行秩等于列秩:$\text{rank}A=\text{rank}A^T$。

| 基本子空间 | 相关性质 |
|---|---|
| 列空间 $C(A)$ | $\dim C(A)=r=\text{#pivot}$ |
| 零空间 $N(A)$ | $\dim N(A)=m-r=\text{#free variables}$ |
| 行空间 $C(A^T)$ | $\dim C(A^T)=r$ |
| 左零空间 $N(A^T)$ | $\dim{N(A^T)}=n-r$ |
一言蔽之,矩阵 $A_{m\times n}$ 描述了向量空间上的线性变换 $T:\mathbb{R}^m\rightarrow\mathbb{R}^n$ ,其蕴含的四个基本子空间囊括了矩阵变换的本质特征。
变换(transformation)
线性变换(linear transformation)
考虑向量空间 $V:\mathbb{R}^n$ 与 $W:\mathbb{R}^m$,选取 $V$ 上的一组基 $B=(\pmb{b}_1,\dots,\pmb{b}_n)$,对 $V$ 内任意向量 $\pmb{x}$,我们有:
\[\begin{cases} \pmb{x}=r_1\pmb{b}_1+\dots+r_n\pmb{b}_n \\ \pmb{x}_B=[r_1,\dots,r_n]^T \end{cases}\]我们知道,矩阵 $A_{m\times n}$ 描述了线性变换 $T:\mathbb{R}^n\rightarrow\mathbb{R}^m$,则矩阵对向量的作用可表示为:
\[T(\pmb{x})=r_1T(\pmb{b}_1)+\dots+r_nT(\pmb{b}_n)=M\pmb{x}_B\]其中 $M=[T(\pmb{b}_1),\dots,T(\pmb{b}_n)]$。可以见得,空间到空间的线性变换,可以借由空间内的一组基来显式表示,这一点在欧式空间内的坐标变换公式 $\pmb{x}=P_B\pmb{x}_B$ 上体现的尤为明显。对于变换后的 $T(\pmb{x})$,可以取 $W$ 内的一组基 $C$ 来表示,即 $T(\pmb{x})_C=M\pmb{x}_B$。

我们记 $\text{Im}T$ 为经过变换 $T$ 后的像(image),$\ker T$ 是像为零元的子空间(kernel,即零空间),如此即可以从线性变换的视角来重新理解秩-零度定理。

再例如多项式上的微分算子事实上也是一种线性变换。取多项式空间上的一组基 $B=(1,x,x^2,\dots,x^n)$,则微分算子可以表示为:
\[D=[\frac{\partial1}{\partial x}_B,\dots,\frac{\partial x^n}{\partial x}_B]= \begin{bmatrix} 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 2 & \cdots & 0 \\ 0 & 0 & 0 & \ddots & \vdots \\ \vdots & \vdots & \vdots & \ddots & n-1 \\ 0 & 0 & 0 & \cdots & 0 \end{bmatrix}\]综上所述,矩阵表征的线性变换,可以用不同的基来显式表示,事实上这些基之间的关系互为同构(isomorphism)。
投影(projection)
投影是复合矩阵表示的一种特殊的线性变换。考虑向量 $\pmb{a}$ 和 $\pmb{b}$,向量 $\hat{\pmb{b}}$ 满足 $\hat{\pmb{b}}-\pmb{b}$ 与 $\pmb{a}$ 正交,这时候我们认为 $\hat{\pmb{b}}$ 是 $\text{span}{\pmb{a}}$ 上与 $\pmb{b}$ 最接近的向量,即 $\pmb{b}$ 在 $\pmb{a}$ 上的投影(projection)。
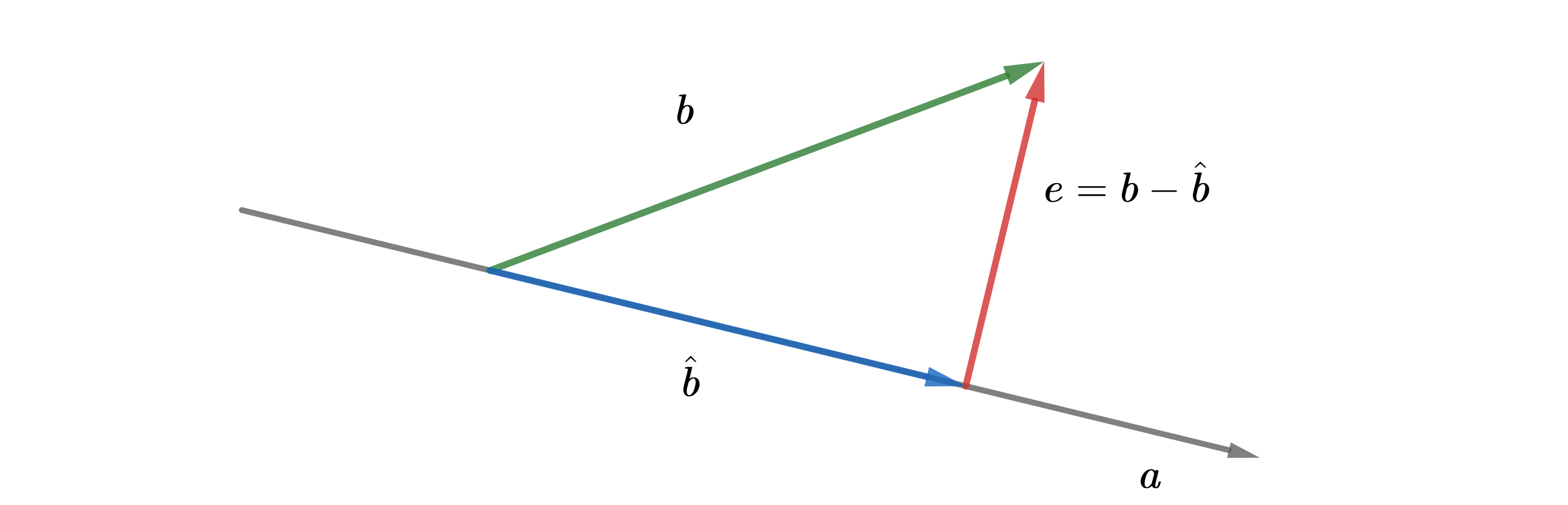
记 $\hat{\pmb{b}}=\lambda\pmb{a}$,我们有:
\[\pmb{a}^T(\pmb{b}-\lambda\pmb{a})=0\Rightarrow\lambda=\frac{\pmb{a}^T\pmb{b}}{\pmb{a}^T\pmb{a}}\] \[\therefore\hat{\pmb{b}}=\lambda\pmb{a}=\pmb{a}\lambda=\pmb{a}\frac{\pmb{a}^T\pmb{b}}{\pmb{a}^T\pmb{a}}=\frac{\pmb{a}\pmb{a}^T}{\pmb{a}^T\pmb{a}}\pmb{b}=P_a\pmb{b}\]如上,我们得到了向量 $\pmb{a}$ 上的投影矩阵 $P_a$,其列空间即 $\pmb{a}$ 所在直线。
最小二乘法(least squared)
考虑矩阵方程 $A\pmb{x}=\pmb{b}$,方程无解即 $\pmb{b}\notin C(A)$。根据上文所阐述的思想,我们需要在 $A$ 的列空间内寻找 $\hat{\pmb{b}}=A\hat{\pmb{x}}$,使得 $\pmb{b}$ 与 $\hat{\pmb{b}}$ 尽量接近,即:
\[\hat{\pmb{x}}=\text{argmin}(\parallel\pmb{b}-A\hat{\pmb{x}}\parallel)\]当 $\pmb{b}$ 和 $\hat{\pmb{b}}$ 最接近时,$\hat{\pmb{b}}$ 即 $\pmb{b}$ 在 $A$ 列空间上的投影。考虑到矩阵的列空间与左零空间互为正交补空间,因此对 $\pmb{b}$ 做正交分解 $\pmb{b}=\hat{\pmb{b}}+\pmb{e}$,必定有 $\pmb{e}\in N(A^T)$,因此:
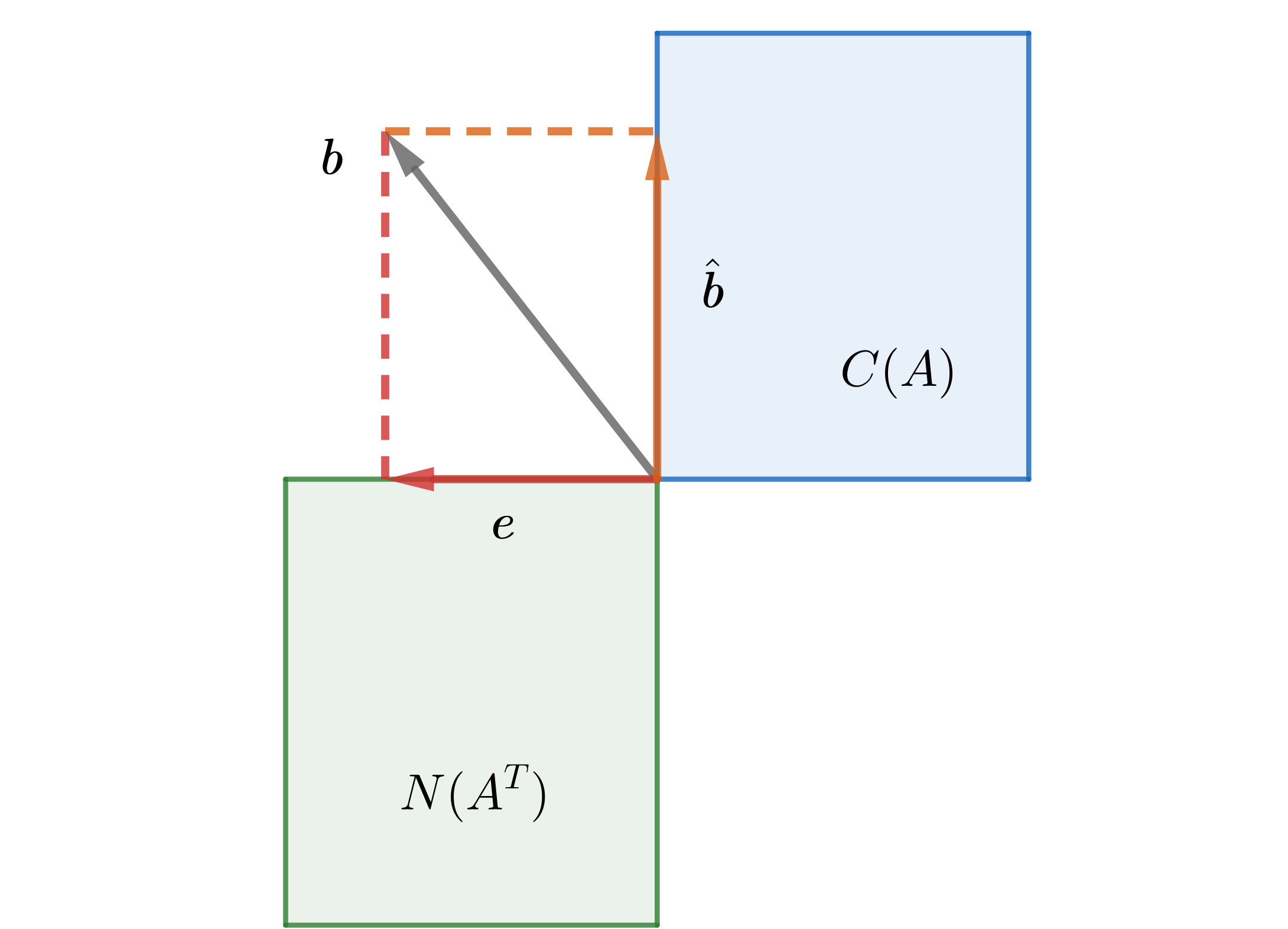
因此矩阵方程 $A^TA\hat{\pmb{x}}=A^T\pmb{b}$ 的解就是我们需要的解,它告诉我们如何寻找 $\pmb{b}$ 在矩阵列空间内的投影。同时我们也找到了关于列空间的投影矩阵 $P_A=A(A^TA)^{-1}A^T$。
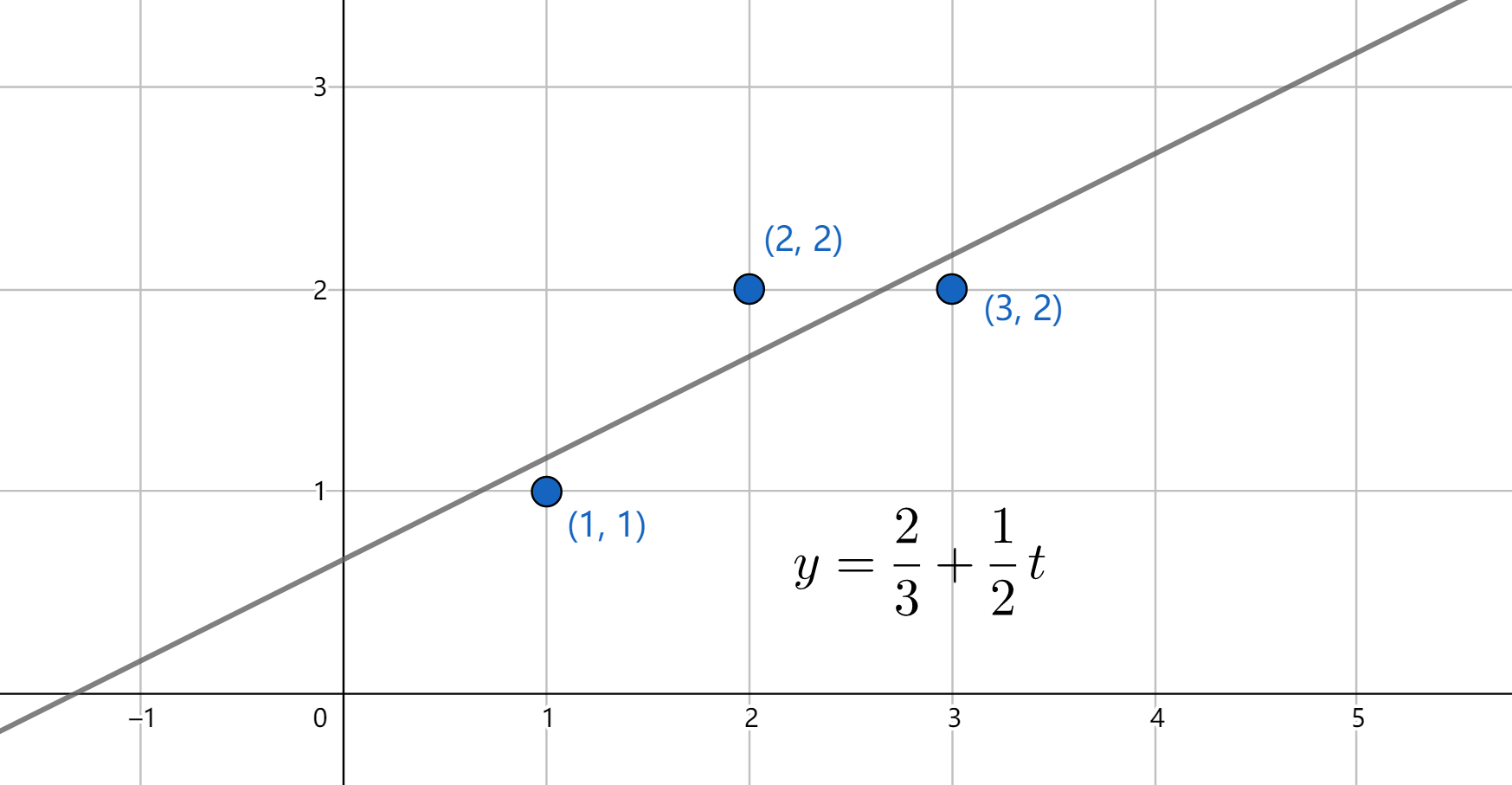
例如,对于点 $(1,1)$,$(2,2)$,$(3,2)$,拟合直线 $y=C+Dt$ 使之与假想过三点的直线最为接近,对此我们有:
\[\begin{cases} C+D=1 \\ C+2D=2 \\ C+3D=2 \end{cases}\Rightarrow \begin{bmatrix} 1 & 1 \\ 1 & 2 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} C \\ D \end{bmatrix}= \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}\Rightarrow A\pmb{x}=\pmb{b}\] \[\therefore A^TA\hat{\pmb{x}}=A^T\pmb{b}\Rightarrow \begin{bmatrix} 3 & 6 \\ 6 & 14 \end{bmatrix} \begin{bmatrix} C \\ D \end{bmatrix}= \begin{bmatrix} 5 \\ 11 \end{bmatrix}\Rightarrow \begin{bmatrix} C \\ D \end{bmatrix}= \begin{bmatrix} 2/3 \\ 1/2 \end{bmatrix}\]最终我们得到了拟合后的直线 $y=\displaystyle\frac{2}{3}+\displaystyle\frac{1}{2}t$。事实上直接考虑 $\min(\parallel\pmb{b}-A\hat{\pmb{x}})$,通过拉格朗日乘数法求解也能得到相同的结果,只是计算量要更为庞大。
关于 $A^TA$,事实上其与 $A$ 拥有相同的零空间,且两者的秩是相等的,有兴趣的读者可以自行证明。
标准正交基(orthonormal basis)
我们把两两相互正交的向量集称为正交集(orthogonal set)。容易证明,正交集是线性无关集,由于正交基的内积特性,选取正交基进行相关计算会十分的便利。其中,列基是单位正交基的矩阵有很多优良的计算性质,粗略地说,不同的标准正交基间仅仅是方向的改变或整体的旋转,因此由标准正交基构成的矩阵具有保长度和保角度的性质。
- $\parallel U\pmb{x}\parallel=\parallel\pmb{x}\parallel$
- $(U\pmb{x})\cdot(U\pmb{y})=\pmb{x}\cdot\pmb{y}$
- $(U\pmb{x})\cdot(U\pmb{y})=0\iff\pmb{x}\cdot\pmb{y}=0$
- $U^TU=I$
格拉姆-施密特法(Graham-Schmidt)可以很快的构造出正交基,它的核心思想是基于投影的正交分解。考虑由一组线性无关的向量组成的基 $B={\pmb{a}_1,\pmb{a}_2,\pmb{a}_3}$,选取 $\pmb{b}_1=\pmb{a}_1$ 作为初始向量,对其他向量依次做正交分解即可快速生成新的正交基 $Q={\pmb{b}_1,\pmb{b}_2,\pmb{b}_3}$,单位化后即可生成标准正交基。
\[\pmb{b}_2=\pmb{a}_2-P_1\pmb{a}_2=\pmb{a}_2-\frac{\pmb{b}_1\pmb{b}_1^T}{\pmb{b}_1^T\pmb{b}_1}\pmb{a}_2=\frac{(\pmb{b}_1,\pmb{a}_2)}{(\pmb{b}_1,\pmb{b}_1)}\pmb{b}_1\] \[\pmb{b}_3=\pmb{a}_3-P_1\pmb{a}_3-P_2\pmb{a}_3=\pmb{a}_3-\frac{(\pmb{b}_1,\pmb{a}_3)}{(\pmb{b}_1,\pmb{b}_1)}\pmb{b}_1-\frac{(\pmb{b}_2,\pmb{a}_3)}{(\pmb{b}_2,\pmb{b}_2)}\pmb{b}_2\]仿射变换(affine transformation)
仿射组合
向量 $\pmb{v}_1,\dots,\pmb{v}_p$ 的仿射组合 $\pmb{y}=c_1\pmb{v}_1+\dots+c_p\pmb{v}_p$ 是一种特殊的线性组合,满足 $\sum c_i=1$。容易证明,$\pmb{y}-\pmb{v}_1$ 事实上也是 $\pmb{v}_2-\pmb{v}_1,\dots,\pmb{v}_p-\pmb{v}_1$ 的线性组合。
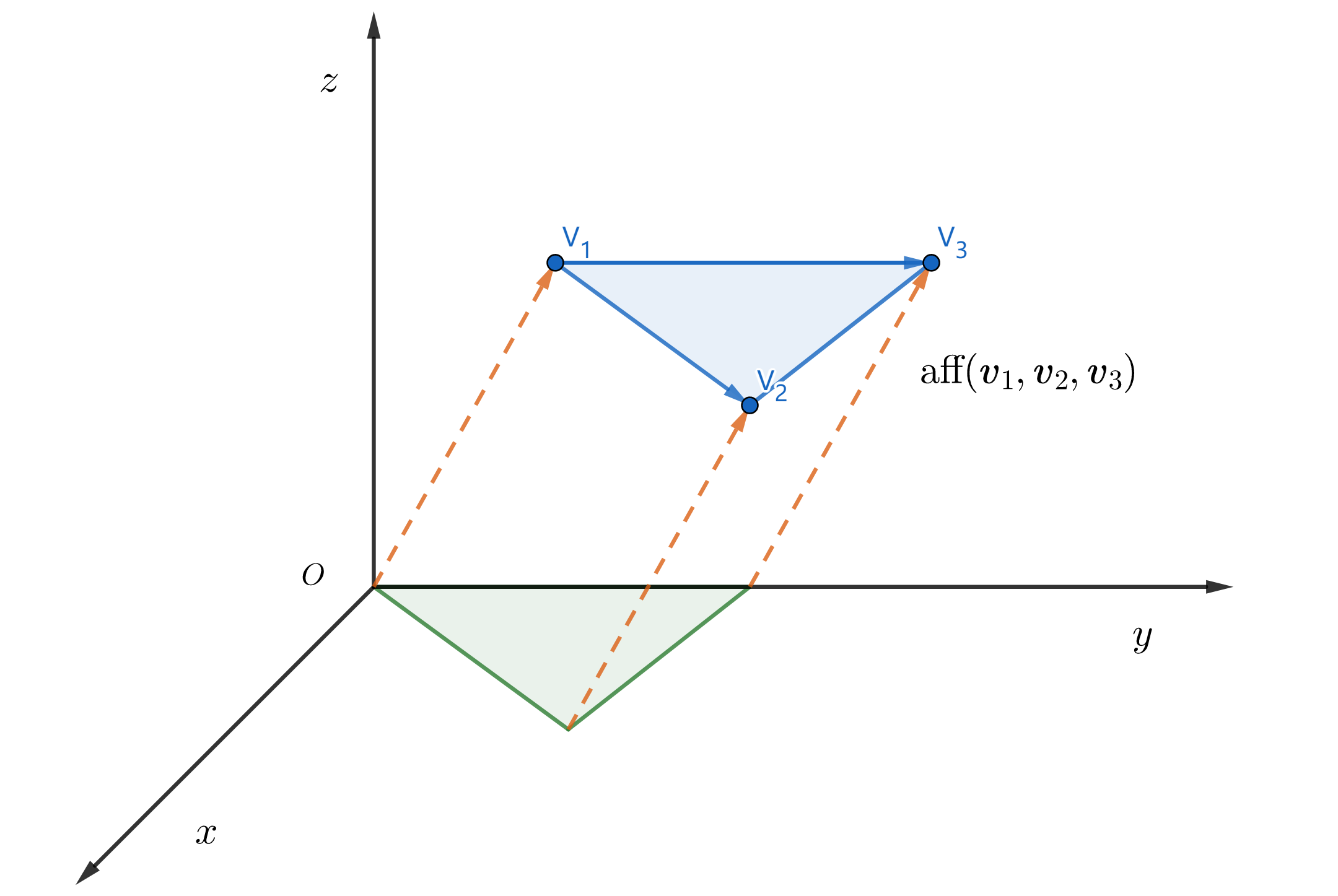
为方便表述,我们将集合 $S$ 中所有点(向量)的所有的仿射组合的集合称为 $S$ 的仿射生成集(仿射包),记为 $\text{aff}(S)$。不难发现,当向量间线性无关时,$\text{aff}(\pmb{v}_1,\pmb{v}_2)$ 表示的是过 $\pmb{v}_1,\pmb{v}_2$ 的直线;$\text{aff}(\pmb{v}_1,\pmb{v}_2,\pmb{v}_3)$ 表示的是过三点的平面。从图例中可以明显的看出,仿射生成集构筑的平面 $\text{aff}(\pmb{v}_1,\pmb{v}_2,\pmb{v}_3)$,事实上与 $\text{span}(\pmb{v}_2-\pmb{v}_1,\pmb{v}_3-\pmb{v}_1)$ 是平行的。
因此,仿射变换生成的平面集,其实质就是线性变换生成的平面集的整体平移,我们可以用 $\pmb{y}=A\pmb{x}+\pmb{b}$ 来描述这种变换。事实上,$A\pmb{x}=\pmb{b}$ 的解集正是 $\mathbb{R}^n$ 的一个仿射子集,与 $A$ 的零空间相平行。
超平面(Hyperplane)
$\text{aff}(S)$ 是由 $S$ 中的点生成的超平面,我们可以用一个线性函数(如 $ax+by=d$,$ax+by+cz=d$)来表示,记作 $[f:d]={\pmb{x}\in\mathbb{R}^n:f(\pmb{x})=d}$。
$f$ 表示的线性变换对应矩阵 $A_{1\times n}$,则 $[f:0]$ 事实上就是 $A$ 的零空间 $N(A)$,$[f:d]$ 可视作 $N(A)$ 的平移,即 $[f:d]=[f:0]+\pmb{b}$。同时,因为 $A$ 亦可看做是行向量,$A\pmb{x}=d$ 的左侧可重新写成内积的形式,即 $[f:d]={\pmb{x}\in\mathbb{R}^n:\pmb{n}\cdot\pmb{x}=d}$。由于 $\text{span}(\pmb{n})=C(A^T)=N(A)^\bot$,$\pmb{n}$ 与 $[f:d]$ 亦正交,我们称之为超平面的法向量,由线性函数的系数组成。
齐次坐标(Homogeneous coordinates)
一个仿射变换可以用 $\pmb{y}=A\pmb{x}+\pmb{b}$ 加以描述。事实上,对该式稍加改写我们就可以用一个简单的线性变换来描述仿射变换:
\[\begin{bmatrix} \pmb{y} \\ 1 \end{bmatrix}= \begin{bmatrix} A & \pmb{b} \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \pmb{x} \\ 1 \end{bmatrix}= \begin{bmatrix} A\pmb{x}+\pmb{b} \\ 1 \end{bmatrix}\]上式表述的线性变换对原始坐标进行了 1-填充,我们称这样的坐标为齐次坐标,用 $\overset{\sim}{\pmb{x}}$ 加以区分。在齐次坐标的视角下我们就可以用单个矩阵 $\overset{\sim}{A}$ 表示的线性变换来代替原本的仿射变换。
\[\begin{cases} \pmb{y}=c_1\pmb{v}_1+\dots+c_p\pmb{v}_p \\ c_1+\dots+c_p=1 \end{cases}\iff \overset{\sim}{\pmb{y}}=c_1\overset{\sim}{\pmb{v}_1}+\dots+c_p\overset{\sim}{\pmb{v}_p}=\overset{\sim}{A}\overset{\sim}{\pmb{x}}\]在 SLAM 中一个最基本的应用便是如何实现坐标平移。引入齐次坐标的概念后我们就可以用一个简单的线性变换来实现仿射变换所表示的这种平移变换。
\[\begin{bmatrix} R & T \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & h \\ 0 & 1 & k \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} x+h \\ y+k \\ 1 \end{bmatrix}\]若 $S={\pmb{v}_1,\dots,\pmb{v}_p}$ 是仿射无关集,则对于 $\text{aff}(S)$ 上的任意一点 $\pmb{p}$,存在唯一坐标 $(c_1,\dots,c_p)$ 使得 $\pmb{p}=c_1\pmb{v}_1+\dots+c_p\pmb{v}_p$,$\sum c_i=1$,我们称该坐标为仿射坐标。
\[\begin{bmatrix} \pmb{p} \\ 1 \end{bmatrix}= c_1\begin{bmatrix} \pmb{v}_1 \\ 1 \end{bmatrix}+\dots+c_p \begin{bmatrix} \pmb{v}_p \\ 1 \end{bmatrix}\]上式事实上是以齐次坐标为基对 $\text{aff}(S)$ 上点的显式表达。由于 $\text{aff}(S)$ 客观上是由 $S$ 中的点生成的超平面,因此该式可看做是以 $S$ 中的所有点为权重对 $\text{aff}(S)$ 上点的插值表示,因此该坐标与物理意义上的重心坐标是一致的。
分解(decomposition)
特征值分解(eigen value decomposition)
特征向量(eigen vector)
在欧氏空间的视角下,矩阵变换可视作对空间内所有的点进行拉伸和旋转,而对于复合后的矩阵(如矩阵的幂),我们很难借助图像来表征这样的复合变换。
但假设存在这样的向量,矩阵对其只进行拉伸变换,我们就可以用拉伸系数的幂来表示矩阵的复合变换。我们称满足 $A\pmb{x}=\lambda\pmb{x}$ 的非零向量 $\pmb{x}$ 为特征向量(eigen vector),拉伸系数 $\lambda$ 为特征值(eigen value)。将特征向量写成如下格式,我们很快就能得到关于特征向量的一个重要结论:对角化定理。
\[\begin{cases} A\pmb{x}_1=\lambda_1\pmb{x}_1 \\ A\pmb{x}_2=\lambda_2\pmb{x}_2 \\ A\pmb{x}_3=\lambda_3\pmb{x}_3 \end{cases}\Rightarrow A\begin{bmatrix} \pmb{x}_1 & \pmb{x}_2 & \pmb{x}_3 \end{bmatrix}= \begin{bmatrix} \pmb{x}_1 & \pmb{x}_2 & \pmb{x}_3 \end{bmatrix} \begin{bmatrix} \lambda_1 & 0 & \cdots & 0\\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \lambda_n \end{bmatrix}\]容易证明,不同特征值对应的特征向量间线性无关(一个方向只有一个拉伸系数),因此由特征向量组成的矩阵 $P$ 一定是可逆的,因此有 $A=PDP^{-1}$,其中 $D=\text{diag}{\lambda_1,\dots,\lambda_n}$,这就是矩阵的特征值分解。
我们已经知道,矩阵对应的线性变换可以借助不同的基来显式表示(通常由列向量组成的基表示),若选取特征向量组成的基 $B={\pmb{x}_1,\dots,\pmb{x}_n}$,结合坐标变换 $\pmb{x}=P\pmb{x}_B$,我们有:
\[\begin{aligned} T_B &= [T(\pmb{x}_1)_B,T(\pmb{x}_2)_B,\dots,T(\pmb{x}_n)_B] \\ &= [(\lambda_1\pmb{x}_1)_B,(\lambda_2\pmb{x}_2)_B,\dots,(\lambda_n\pmb{x}_n)_B] \\ &= [P^{-1}A\pmb{x}_1,P^{-1}A\pmb{x}_2,\dots,P^{-1}A\pmb{x}_n] \\ &= P^{-1}AP=D \end{aligned}\]如上,我们知晓 $\pmb{x}\mapsto A\pmb{x}$ 和 $\pmb{u}\mapsto D\pmb{u}$ 事实上是等价的,仅仅是同一个线性变换的不同基的表示形式。我们称满足 $A=PBP^{-1}$ 的矩阵 $A,B$ 互为相似矩阵(similar bmatrix)。同时我们也会发现,使用特征向量作为基来描述矩阵表示的线性变换,在计算上会带来极大的便利。
动力系统
考虑如下应用场景:若每年要统计一个城市及其郊区的人口分布问题,如 $x_0=[0.60,0.40]^T$ 表示初始有 $60\%$ 的人口住在城市,$40\%$ 的人口住在郊区。假设每年有 $5\%$ 的城市人口流动到郊区,有 $3\%$ 的人口流动到城市,我们可以用矩阵方程来表征上述一阶差分动力系统:
\[\pmb{x}_{k+1}=M\pmb{x}_k= \begin{bmatrix} 0.95 & 0.03 \\ 0.05 & 0.97 \end{bmatrix}^{k+1} \begin{bmatrix} 0.60 \\ 0.40 \end{bmatrix} ,\quad k=0,1,2\dots\]令 $\det(A-\lambda I)=0$,可以求出 $M$ 的特征值 $\lambda_1=1$,$\lambda_2=0.92$,回代即可求得其对应的特征向量 $\pmb{v}_1=[3,5]^T$,$\pmb{v}_2=[1,-1]^T$。以特征向量为基底表示初始向量,我们就可以很快求出矩阵的幂对原始向量的影响:
\[\pmb{x}_1=A\pmb{x}_0=c_1\lambda_1\pmb{v}_1+c_2\lambda_2\pmb{v}_2=0.125\pmb{v}_1+0.225\cdot(0.92)^k\pmb{v}_2\] \[\lim_{k\rightarrow\infty}\pmb{x}_k=0.125\pmb{v}_1=\begin{bmatrix} 0.375 \\ 0.625 \end{bmatrix}\]如上,利用矩阵的特征值分解我们可以快速求出矩阵的幂对向量的影响。事实上这是一个由一阶差分方程刻画的经典的马尔可夫链(Markov chain),该链经长期行为后最终收敛至稳态(steady state)。
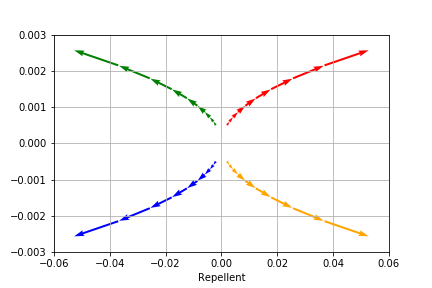
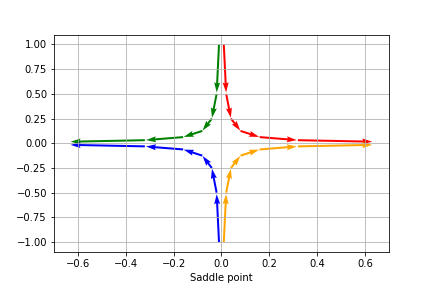
对于类似的一阶差分方程,我们亦可以借助点的轨迹来模拟动力系统的变化情况。下图模拟了三类经典的动力系统所代表的点的轨迹。
\[A=\begin{bmatrix} 0.8 & 0 \\ 0 & 0.64 \end{bmatrix}\quad \pmb{x}_0= \begin{bmatrix} \pm0.2 \\ \pm0.3 \end{bmatrix}\quad \text{吸引子(Attractor)}\]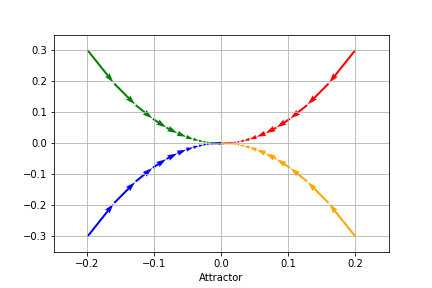
复特征向量
遗憾的是,并不是所有的矩阵都有完备的实特征向量组,考虑二阶旋转阵 $R_2$($\theta=\pi/2$),显然在 $R_2$ 作用下二维平面内不存在仅被拉伸的实向量。但如果将特征向量的概念从实数域扩展至复数域,我们很容易就能得到 $R_2$ 的两个复特征值 $i$ 和 $-i$,这与我们对复数 $i$ 表示旋转的认知是一致的。
\[\det(R_2-\lambda I)=0\Rightarrow \begin{cases} \pmb{x}=\begin{bmatrix} \pm i \\ 1 \end{bmatrix} \\ \lambda=\pm i \end{cases}\]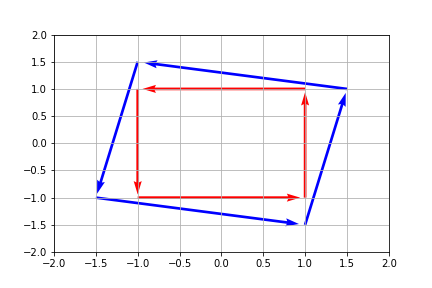
考虑方阵 $A_{n\times n}$,由代数基本定理我们知道该阵的特征方程 $\det(A-\lambda I)$ 必有 $n$ 个复根(包含重根),因此在复数域内矩阵的性质可由矩阵的复特征向量完全表述。同时,对实矩阵 $A_{n\times n}$ 有 $\overline{A\pmb{x}}=A\overline{\pmb{x}}$,因此实矩阵的特征值和特征向量总是共轭成对出现的。
我们已经知道矩阵描述了一种旋转或拉伸的线性变换,事实上在复数域我们可以借助 $i$ 实现矩阵的旋转-拉伸分解。考虑以下二阶阵 $C$,它的特征值 $\lambda=a\pm bi$,记 $r=\vert\lambda\vert$,我们有:
\[C=\begin{bmatrix} a & -b \\ b & a \end{bmatrix}=\begin{bmatrix} r & 0 \\ 0 & r \end{bmatrix}\begin{bmatrix} \cos\phi & -\sin\phi \\ \sin\phi & \cos\phi \end{bmatrix}\]其中 $\phi$ 是 $\lambda$ 的幅角。如上任意一个满足 $C$ 格式的矩阵都可以分解为一个表示拉伸的对角阵和旋转阵的乘积。更一般的,对于所有实二阶阵 $A_{2\times 2}$,记 $\lambda=a-bi$,$A\pmb{v}=\lambda\pmb{v}$ 我们有:
\[\begin{cases} A(\text{Re}\pmb{v})=a\text{Re}\pmb{v}+b\text{Im}\pmb{v} \\ A(\text{Im}\pmb{v})=-b\text{Re}\pmb{v}+a\text{Im}\pmb{v} \end{cases}\Rightarrow A\begin{bmatrix} \text{Re}\pmb{v} & \text{Im}\pmb{v} \end{bmatrix}= \begin{bmatrix} \text{Re}\pmb{v} & \text{Im}\pmb{v} \end{bmatrix} \begin{bmatrix} a & -b \\ b & a \end{bmatrix}\]记 $P=[\text{Re}\pmb{v}, \text{Im}\pmb{v}]$,我们有 $AP=PC$,即 $A=PCP^{-1}$,此谓二阶矩阵的旋转-拉伸分解(RSD),对于更高阶矩阵亦有同样的分解方式,在此不做赘述。
对称矩阵(symmetric matrix)
我们在投影中最早遇到关于对称矩阵的概念,$A^TA$ 和 $AA^T$ 就是经典的对称矩阵,事实上对称矩阵具有很多优良的计算性质。考虑 $A^T=A$ 和复向量 $\pmb{x}$,我们有:
\[q=\overline{\pmb{x}}^TA\pmb{x}=(\overline{\pmb{x}}^TA\pmb{x})^T=\pmb{x}^TA\overline{\pmb{x}}=\overline{q}\]显然 $q$ 是实数,考虑 $A\pmb{x}=\lambda\pmb{x}$,我们有 $\overline{\pmb{x}}^TA\pmb{x}=\lambda\overline{\pmb{x}}^T\pmb{x}$,因此对称矩阵的特征值必为实数,对于对称矩阵 $A_{n\times n}$,其必有 $n$ 个实特征值,必可被正交对角化为 $QDQ^T$。
\[A=QDQ^T=\lambda_1\pmb{q}_1\pmb{q}_1^T+\dots+\lambda_n\pmb{q}_n\pmb{q}_n^T\]后式被称为对称矩阵的谱分解(spectral theorem),可以理解为 $A$ 在其特征向量上投影的叠加。
二次型(quadratic form)
主轴定理(principal axis theorem)
二次型是一种特殊的线性变换,表达式为 $Q(\pmb{x})=\pmb{x}^TA\pmb{x}$,可看做是定义在 $\mathbb{R}^n$ 上的一类函数。其中 $A$ 是对称矩阵,例如:
\[Q(\pmb{x})=\begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix} 1 & -4 \\ -4 & -5 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}=x_1^2-8x_1x_2-5x_2^2\]若 $A=I$ 就可得到最简单的二次型 $Q(\pmb{x})=\pmb{x}^TI\pmb{x}=\parallel\pmb{x}\parallel$。显然,没有交叉项的二次型($A$ 为对角阵)具备更加简洁的性质。幸运的是,我们可以通过变量替换的方式消去一般二次型中的交叉项。
考虑变量替换 $\pmb{x}=P\pmb{y}$,$Q(\pmb{x})=\pmb{x}^TA\pmb{x}=\pmb{y}^TP^TAP\pmb{y}$,问题转换为使 $P^TAP$ 对角化,这对于对称矩阵 $A$ 来说是显然的,其可以通过正交对角化为 $PDP^T$ 求出我们需要的 $P$。
\[\det(A-\lambda I)=0\Rightarrow\begin{cases} \lambda_1=3 \\ \lambda_2=-7 \end{cases}\Rightarrow P=\begin{bmatrix} 2/\sqrt{5} & 1/\sqrt{5} \\ -1/\sqrt{5} & 2/\sqrt{5} \end{bmatrix}\]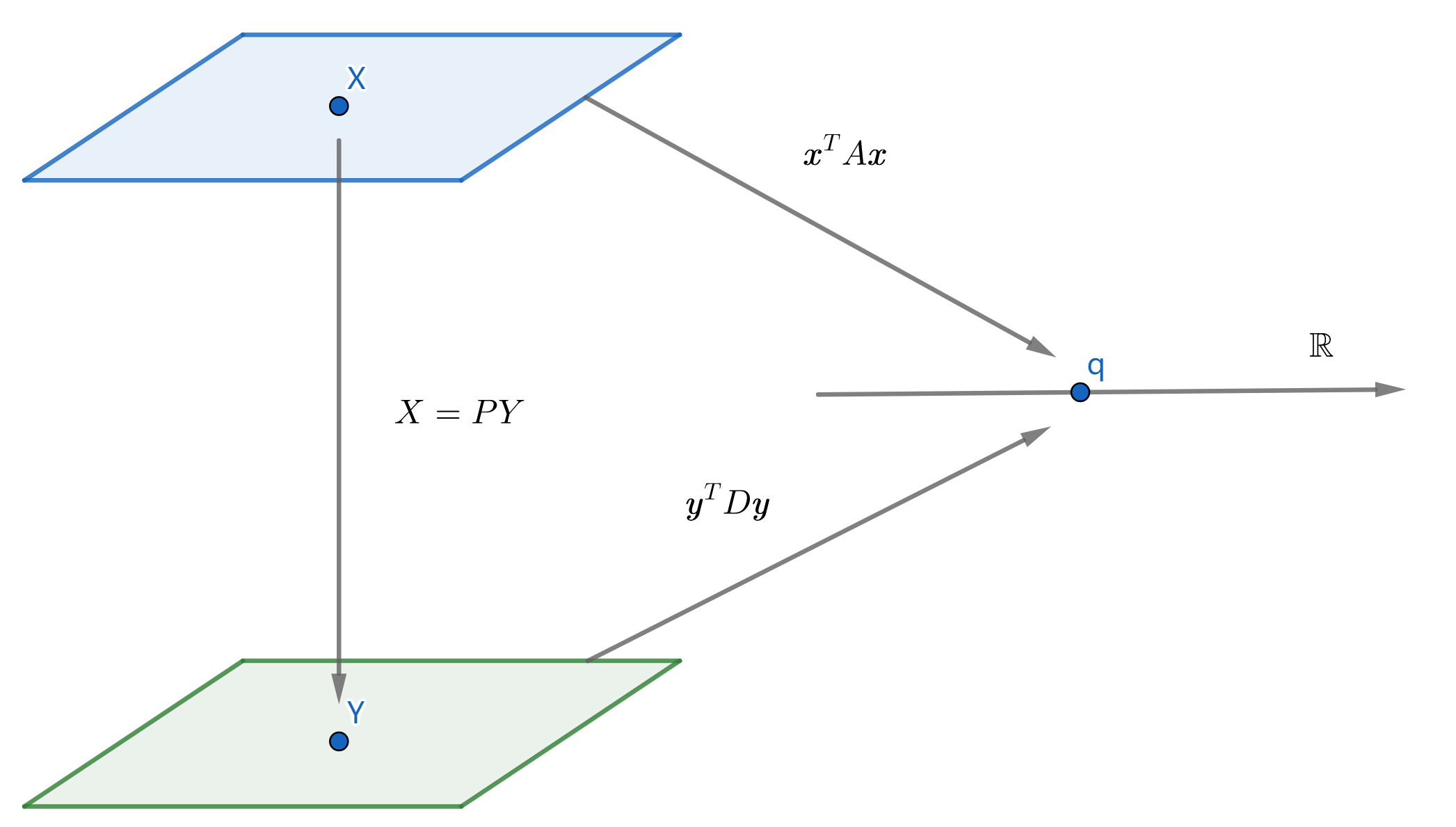
$P$ 是由标准正交基构成的矩阵,因此 $\pmb{x}$ 具备的几何性质与 $\pmb{y}$ 基本一致,我们可以直接研究 $\pmb{y}$ 来代替原本的二次型。与谱分解类似,我们用二次型针对 ${y_1,\dots,y_n}$ 的拉伸系数来表征二次型的作用,这就是主轴定理。
\[Q(\pmb{x})=\pmb{x}^TA\pmb{x}=\pmb{y}^TD\pmb{y}=\lambda_1y_1^2+\dots+\lambda_n y_n^2\]此外,当对称阵 $A_{n\times n}$ 满足 $\forall\pmb{x}\in\mathbb{R}^n$,$\pmb{x}^TA\pmb{x}>0$ 时,$A$ 又被称作正定矩阵,它有以下性质:
- 所有的特征值 $\lambda$ 大于零
- 所有的子行列式大于零
- 所有主元大于零
当 $A$ 是正定矩阵时,$\pmb{x}^TA\pmb{x}=1$ 表示的图形是一个椭型曲线(ellipse),在 $\mathbb{R}^2$ 上它是一个椭圆:
\[Q(\pmb{x})=\begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} 5 & 4 \\ 4 & 5 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}=5x^2+8xy+5y^2=1\]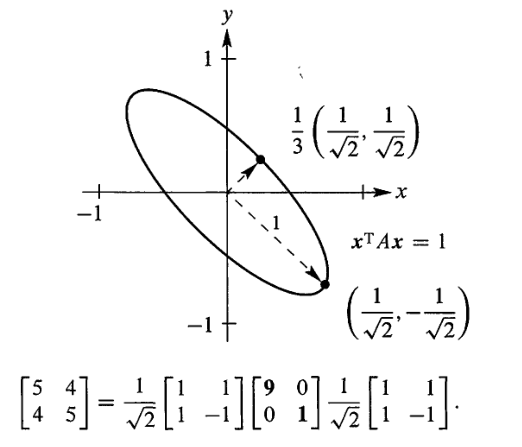
很明显,椭圆的轴方向与 $A$ 特征向量的方向一致,半轴长刚好是 $A$ 特征值的倒数,这个性质亦可推广至 $\mathbb{R}^n$ 上所有的椭圆曲线。
带限二次型最值问题
工程中遇到的所有关于二次型最值优化问题,均可归结为单位向量在二次型中的最值问题,即:
\[\begin{aligned} &\max\quad Q(\pmb{x}) \\ &s.t.\quad \pmb{x}^T\pmb{x}=1 \end{aligned}\]对于无交叉项的二次型我们很容易就能求得它们的最值,且与其对应的主轴长相关。考虑一般类二次型 $Q(\pmb{x})=\pmb{x}^TA\pmb{x}=\pmb{y}^TD\pmb{y}$,注意到 $\parallel\pmb{x}\parallel=\parallel P\pmb{y}\parallel=\parallel\pmb{y}\parallel$(粗略地说,单位正交基仅起到旋转作用),因此求一般二次型的最值等价于求变量替换后得到的无交叉项二次型的最值。记 $\pmb{x}=P\pmb{y}$,$P=[\pmb{u}_1,\pmb{u}_2,\pmb{u}_3]$,若 $D$ 按特征值降序排列组成,则对于无交叉项二次型来说,取得最值的向量为 $\pmb{y}=[1,0,0]^T=\pmb{e}_1$,最值为 $\lambda_1$。
\[\pmb{e}_1^TD\pmb{e}_1=\pmb{u}_1A\pmb{u}_1=\lambda_1\]容易证明,二次型的取值范围与其对应主轴有关:
\[\begin{cases} \pmb{x}^TA\pmb{x} \\ \pmb{x}^T\pmb{x}=1 \end{cases}\Rightarrow\lambda_{\text{min}}\leq Q(\pmb{x})\leq\lambda_{\text{max}}\]增加更多关于正交相关的限制,我们可以得到一个有趣的结论:
\[\begin{aligned} &\max\quad Q(\pmb{x}) \\ &s.t.\quad\begin{cases} \pmb{x}^T\pmb{x}=1 \\ \cdots\cdots \\ \pmb{x}T\pmb{u}_{k-1}=0 \end{cases} \end{aligned}\]由于 $\pmb{x}\in\text{span}(\pmb{u}_k,\dots,\pmb{u}_n)$,不难证明,此时 $\max{(\pmb{x}^TA\pmb{x})}=\lambda_k$。
奇异值分解(singular value decomposition)
我们已经知道,并不是所有的矩阵都可以进行实对角化,因此我们无法用一组基的拉伸系数来表征这样的矩阵。但是,效仿二次型中的主轴定理,我们完全可以从主轴变化的视角来重新审视矩阵表示的线性变换。考虑如下矩阵 $A_{2\times3}$,它表示的线性变换 $T:\pmb{x}\rightarrow A\pmb{x}$ 能够将 $\mathbb{R}^3$ 中的单位球变换为 $\mathbb{R}^2$ 上的椭圆:
\[A=\begin{bmatrix} 4 & 11 & 14 \\ 8 & 7 & -2 \end{bmatrix}\]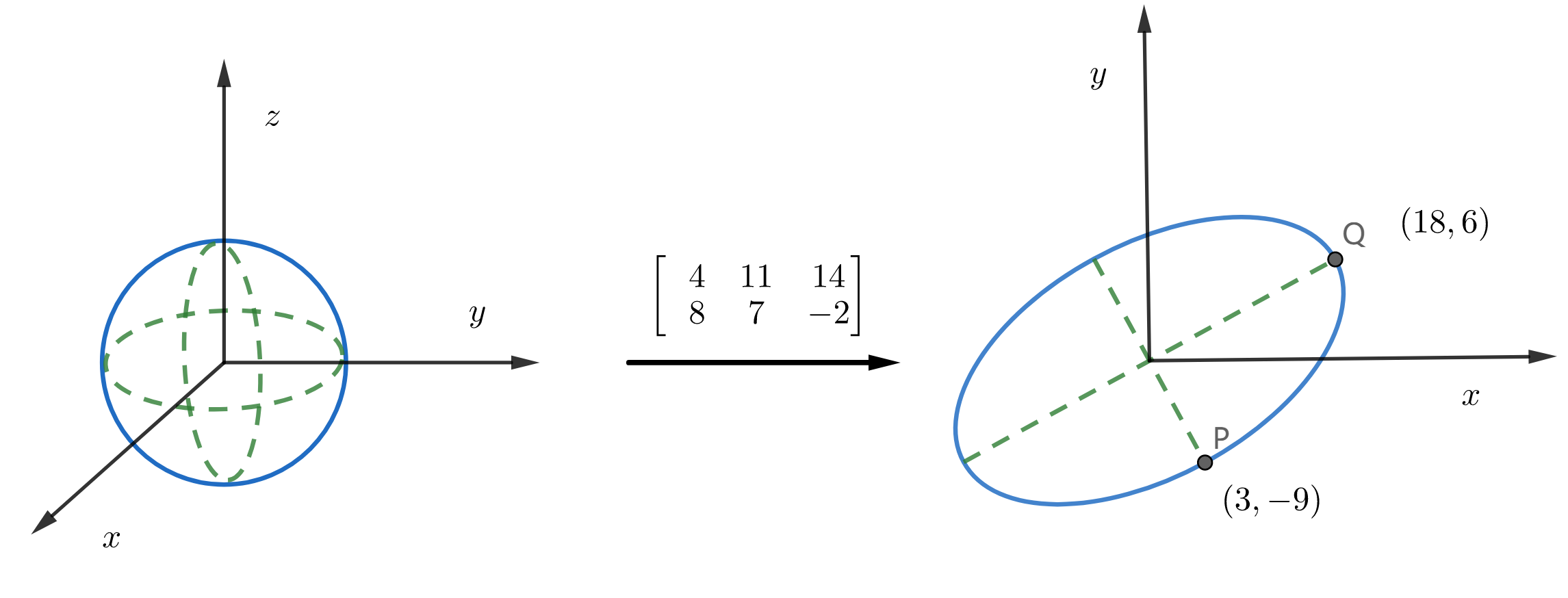
因此 $A$ 表示的线性变换,完全可以由变换后椭圆曲线的主轴来表征。主轴长即 $\max\parallel A\pmb{x}\parallel$,等价于求 $\max\parallel A\pmb{x}\parallel^2=\max(\pmb{x}^TA^TA\pmb{x})$,这正是我们熟悉的二次型,最值即其特征值,与主轴长度相对应:
\[A^TA=\begin{bmatrix} 80 & 100 & 40 \\ 100 & 170 & 140 \\ 40 & 140 & 200 \end{bmatrix}\Rightarrow\begin{cases} \lambda_1=360 \\ \lambda_2=90 \\ \lambda_3=0 \end{cases}\Rightarrow \pmb{v}_1=\begin{bmatrix} 1/3 \\ 2/3 \\ 2/3 \end{bmatrix}^T, \pmb{v}_2=\begin{bmatrix} -2/3 \\ -1/3 \\ 2/3 \end{bmatrix}^T\] \[A\pmb{v}_1=\begin{bmatrix} 18 \\ 6 \end{bmatrix}\qquad A\pmb{v}_2=\begin{bmatrix} 3 \\ -9 \end{bmatrix}\]记 ${\pmb{v}_1,\dots,\pmb{v}_n}$ 是 $A^TA$ 特征向量组成的单位正交基,由于 $\parallel A\pmb{v}_i\parallel=\pmb{v}_i^TA^TA\pmb{v}_i=\lambda_i\geq0$,我们记 $\sigma_i=\sqrt{\lambda_i}$ 为 $A$ 的奇异值,$\sigma_i$ 正好对应经 $A$ 变换后的主轴长度 $\parallel A\pmb{v}_i\parallel$。更进一步,若 $A$ 有 $r$ 个非零奇异值,则 ${A\pmb{v}_1,\dots,A\pmb{v}_r}$ 是 $C(A)$ 上的正交基,且 $r=\text{rank}A=\dim C(A)$。
对 $A\pmb{v}_i$ 单位化就可得到一组新的标准正交基 ${\pmb{u}_1,\dots,\pmb{u}_n}$:
\[\pmb{u}_i=\frac{A\pmb{v}_i}{\parallel A\pmb{v}_i\parallel}=\frac{1}{\sigma_i}A\pmb{v}_i\Rightarrow A\pmb{v}_i=\sigma_i\pmb{u}_i\]将右式写成矩阵形式我们就得到了一般矩阵的奇异值分解:
\[A\begin{bmatrix} \pmb{v}_1 & \cdots & \pmb{v}_n \end{bmatrix}=\begin{bmatrix} \sigma_1\pmb{u}_1 & \cdots & \sigma_r\pmb{u}_r & \cdots & 0 \end{bmatrix}=\begin{bmatrix} \pmb{u}_1 & \cdots & \pmb{u}_m \end{bmatrix}\begin{bmatrix} \sigma_1 & \cdots & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \cdots & 0 \\ 0 & 0 & \sigma_r & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & 0 \end{bmatrix}\] \[AV_{n\times n}=U_{m\times m}\Sigma_{m\times n}\Rightarrow A=U\Sigma V^T\]之所以不能对 $A$ 进行特征值分解的原因,我们在 $A$ 的奇异值中已一窥真理。零奇异值的存在让 $A$ 在这个方向上的拉伸能力消失了,以线性变换的视角来看,正如上文中 $\mathbb{R}^3\rightarrow\mathbb{R}^2$ 的变换,可理解为维度的坍缩。主轴组成的基不能完全描述这种变换,剩余的部分被藏在了零空间内,因此我们才借助零空间的正交补空间来补充描述矩阵表征的变换:
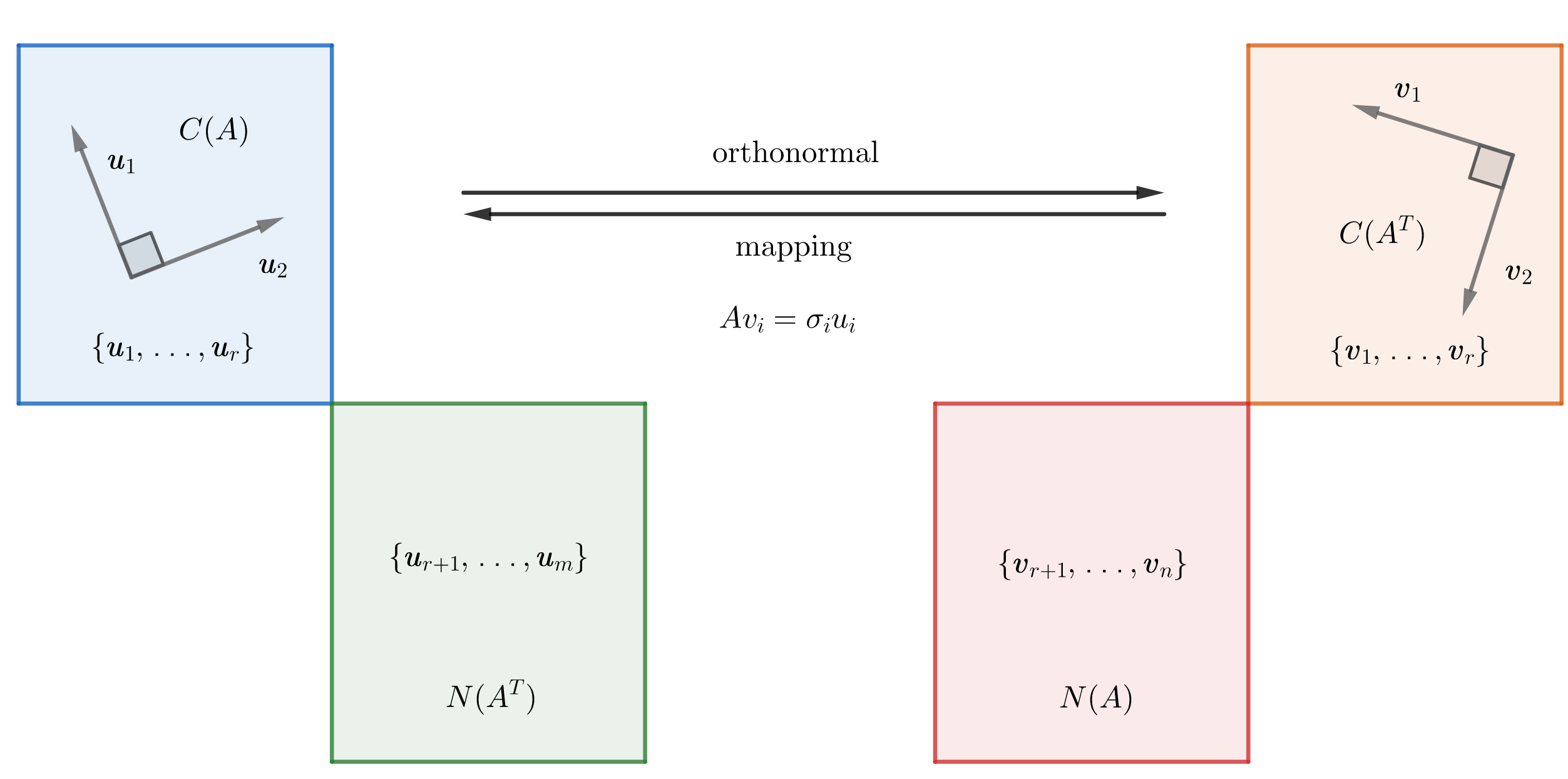
如上,我们结合了矩阵基本子空间的概念,以主轴为关键词引入了矩阵的奇异值分解。正如我们用基(坐标)来描述空间一样,用主轴的拉伸变换来描述矩阵表征的线性变换无疑是简化了我们对变换的理解。在实际计算中我们通常会使用下面两个公式来加快矩阵奇异值的求解:
\[\begin{cases} A^TA=V\Sigma^2V^T\Rightarrow V,\sigma^2 \\ AA^T=U\Sigma^2U^T\Rightarrow U \end{cases}\]Bonus: 伪逆(pseudo-inverse)
在矩阵的奇异值分解中,当 $\Sigma$ 含零元行/列时,消去分解式中冗余的零我们可以得到更为简洁的分解式:
\[A_{m\times n}=\begin{bmatrix} U_r & U_{m-r} \end{bmatrix} \begin{bmatrix} D & \pmb{0} \\ \pmb{0} & \pmb{0} \end{bmatrix} \begin{bmatrix} V_r^T \\ V_{n-r}^T \end{bmatrix}=U_rDV_r^T\]此时 $D$ 为满秩状态,定义 $A^+=V_rD^{-1}U_r^T$,$A^+$ 被称作矩阵的伪逆。容易证明 $AA^+=U_rU_r^T$ 是 $C(A)$ 的投影阵,$A^+A=V_rV_r^T$ 是 $C(A^T)$ 的投影阵。基于伪逆投影的性质,我们可以得到很多有趣的结论,比如在求解线性方程组时,若 $A\pmb{x}=\pmb{b}$ 相容,则 $\pmb{x}^+=A^+\pmb{b}$ 是最小长度解;不相容则是最小长度最小二乘解,有兴趣的读者可自行证明,关于伪逆的其他性质这里暂且不表。