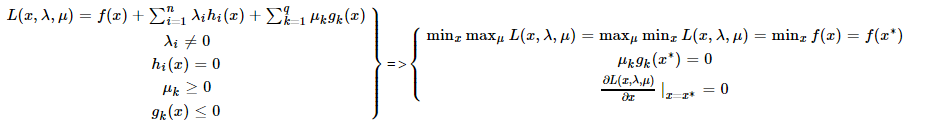| 前导 |
|---|
| 拉格朗日乘数法 |
| KKT 约束条件 |
作为一种优化算法,拉格朗日乘数法主要用于解决约束优化问题。它的基本思想就是通过引入拉格朗日乘子将含有 $n$ 个变量 $k$ 个约束条件的约束优化问题转换为含有 $n+k$ 个变量的无约束优化问题。拉格朗日乘子背后的几何意义是约束方程的梯度线性组合的系数。
\[\min f(x, y, z)\quad\max f(x, y, z)\] \[s.t.\quad g(x, y, z)={\rm C}\]拉乘的基本型是求函数 $z=f(x, y)$ 在满足 $g(x, y)={\rm c}$ 下的条件极值,可转化为函数 $L(x, y, \lambda)=f(x, y)+\lambda(g(x, y)-{\rm c})$ 的无条件极值问题:
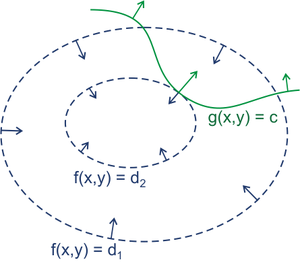
如图,在约束线 $g(x, y)$ 存在的前提下我们很容易就能找到 $f(x, y)$ 等值线簇出现极值的位点,该点处 $f$ 和 $g$ 的梯度向量平行,即:
\[\nabla[f(x, y)+\lambda(g(x, y)-{\rm c})]=0\]因此我们将拉乘的函数形式写为 $L(x, y, \lambda)=f(x, y)+\lambda(g(x, y)-{\rm c})$,对每个分量求偏导令其为零对应的是平行的梯度向量,而对拉格朗日乘子求偏导即为原始的约束条件,联立解一个 $n+k$ 阶的方程组即可求出系数 $\lambda$ 和切点 $(x, y)$。
现实生活中遇到的问题多为不等式约束,在引入 KKT 条件后我们亦可用拉乘解决不等式约束的优化问题。为了容易理解,我们举一个例子说明 KKT 条件的由来:
\[L(x, \mu)=f(x)+\sum_k\mu_kg_k(x)\quad\mu_k\geq0, g_k(x)\leq0\]显然 $\mu g(x)=0$,对上式求含参最优解可得:
\[\max_\mu L(x, \mu)=f(x)\] \[\max_\mu\min_xL(x, \mu)=\min_x\max_\mu L(x, \mu)=\min_xf(x)\]$\max_\mu\min_xL$ 和 $\min_x\max_\mu L$ 互为对偶问题,上式表明在满足一定条件下,对偶的解以及 $\min_xf(x)$ 是相同的,且在最优解处 $\mu g(x^*)=0$,代入上式有:
\[\max_\mu L(x^*, \mu)=\max_\mu\min_xL(x, \mu)=f(x^*)\] \[\Longrightarrow\frac{\partial L(x, \mu)}{\partial x}=0\quad x=x^*\]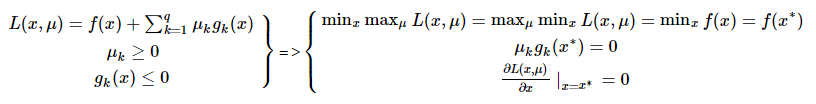
如上,KKT 条件是拉格朗日乘数法的泛化,在引入新的约束条件下就可保证在不等约束下最优化的解仍在等式约束的相同边界上。