| 前导 |
|---|
| 离散时间信号的傅里叶分析 |
| 系统傅里叶分析 |
| 采样 |
离散时间信号的傅里叶分析
基本定义
类比连续时间信号的傅里叶变换我们可以推出离散时间信号的傅里叶变换(DTFT):
\[X(\omega)=\sum_{n=-\infty}^{\infty}x[n]e^{-j\omega n}=X(\omega+2\pi)\]因此离散时间信号的傅里叶变换是周期的,组成 $x[n]$ 的正弦分量的正频率范围为 $0$ ~ $\pi$。DTFT 反变换如下:
\[x[n]=\frac{1}{2\pi}\int_0^{2\pi}X(\omega)e^{jn\omega}{\rm d}\omega\]常见DTFT变换对
| 常见DTFT变换对 |
|---|
| $a^nu[n]\leftrightarrow \displaystyle\frac{1}{1-ae^{-j\omega}}$ |
| $\delta[n]\leftrightarrow1$ |
| $1\leftrightarrow2\pi\displaystyle\sum_{k=-\infty}^\infty\delta(\omega-2\pi k)$ |
| $e^{j\omega_0n}\leftrightarrow2\pi\displaystyle\sum_{k=-\infty}^\infty\delta(\omega-2\pi k-\omega_0)$ |
- 离散 1 的变换对通过反变换证明,此处可一窥截止频率的概念
系统傅里叶分析
系统响应函数
在研究系统时我们一般采用黑盒测试的方法,向系统输入已知信号,通过系统的反馈来研究系统的特征。因此,系统的冲激响应 $h(t)$ 可以完全表征系统的特征。
\[y(t)=x(t)*h(t)\qquad Y(\omega)=X(\omega)H(\omega)\]$H(\omega)$ 可写成幅度和相位谱的合成 $H(\omega)=\vert H(\omega)\vert e^{j\theta}$。从上述系统的频域表示可以看输出,冲激响应仅仅是改变了输入信号的相位和幅度特性:
\[|Y(\omega)|=|X(\omega)|\cdot |H(\omega)|\qquad\angle Y(\omega)=\angle X(\omega)+\angle H(\omega)\]由傅里叶变换式我们易知,$e^{j\omega_0t}$ 是线性时不变系统的特征函数:
\[y(e^{j\omega_0t})=h(t)*e^{j\omega_0t}=H(\omega_0)e^{j\omega_0t}\]例如向系统输入信号 $x(t)=\cos\omega_0t$,我们即可很直观的看出系统响应函数对输入信号幅度和相位的影响:
\[\begin{aligned} y(t) &= \frac{e^{j\omega_0t}+e^{-j\omega_0t}}{2}*h(t) \\ &= \frac{1}{2}[H(\omega_0)e^{j\omega_0t}+H(-\omega_0)e^{-j\omega_0t}] \\ &= \frac{1}{2}[|H(\omega_0)|e^{j\theta}e^{j\omega_0t}+|H(\omega_0)|e^{-j\theta}e^{-j\omega_0t}] \\ &= |H(\omega_0)|\cos(\omega_0t+\theta) \end{aligned}\]而失真,即信号在传输过程中相位特性或幅度特性发生改变。因此,狭义的不失真条件是系统的相位特性是线性的(离散时间还要保证相位特性的斜率是整数)
- 时域表征:$h(t)=k\delta(t-t_0)$
- 频域表征:$H(j\omega)=ke^{-j\omega t_0}$
- 幅度和相位:$\vert H(j\omega)\vert=k\quad \angle H(j\omega)=-\omega t_0$
输入 $x(t)$ 系统的反馈为 $y(t)=kx(t-t_0)$。通常,系统若在被传输信号的带宽范围内满足不失真条件即可认为是不失真系统。
对于一般的线性时不变系统表征的微分方程,我们可以通过解特征方程、时域分析和频域分析的方式解出系统的响应函数。系统的频域响应又可以通过部分分式展开的方式分解为多个一阶和二阶系统的叠加,因此我们只需关注一阶和二阶系统的响应特征即可。
\[\sum_{k=0}^Na_k\frac{d^ky}{dt^k}=\sum_{k=0}^Mb_k\frac{d^kx}{dt^k}\Longrightarrow H(\omega)=\frac{Y(\omega)}{X(\omega)}\]Hint: 对于简单的 FIR 系统可以利用定义直接输入单位冲激信号快速得出系统的频率响应。
一阶连续时间系统
一阶连续时间系统的微分方程表示如下:
\[\tau\frac{dy(t)}{dt}+y(t)=x(t)\]对两侧做傅里叶变换即可得到 $H(j\omega)=\displaystyle\frac{Y(j\omega)}{X(j\omega)}=\displaystyle\frac{1}{j\omega\tau+1}$,$h(t)=\displaystyle\frac{1}{\tau}e^{-t/\tau}u(t)$
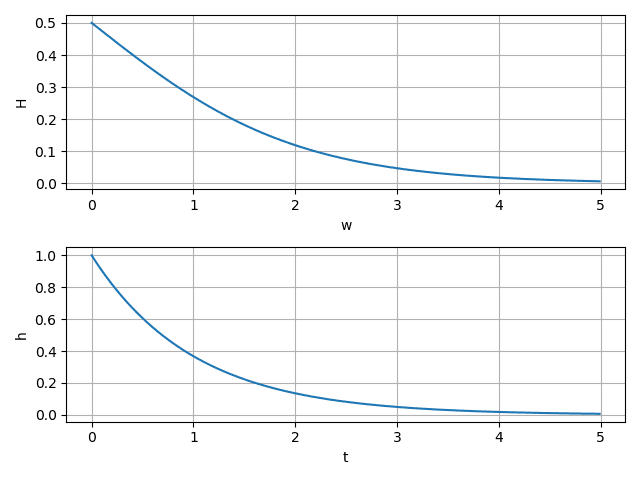
由图可见,$\tau$ 越小,$h(t)$ 下降越快,系统响应速度就越快,系统失真越小。
实践中我们还会研究系统的阶跃响应 $s(t)=h(t)*u(t)=(1-e^{-t/\tau})u(t)$。
而二阶连续时间系统如典型的弹簧系统,其三种状态,欠阻尼(带通)、临界阻尼(低通)、过阻尼(低通)我们已经很熟悉了,不再赘述。阻尼参数使二阶连续时间系统具有选频特性。
实践中我们通过渐近线和点取样的方式画 bott 图分析频率特性。
理想滤波器
理想滤波器用于过滤我们需要的频率信号,要注意理想滤波器是物理不可实现的(非因果)
- 全通:系统的幅频特性是一个常数
- 低通:频率 0 附近的信号可通过,$h(\omega)=\rho(\omega)$
- 高通:可由常数频谱减去低通得到
- 带通:某个频域范围内可通过,可由低通调频得到
- 带阻:某个频域范围内不可通过
对离散时间信号来说,频率在 $\pi$ 的偶数倍附近为低频,奇数倍为高频。
采样
采样定理
一般来说,大部分离散时间信号均可由连续时间信号采样得来。但要注意,一组离散的样本值并不能唯一确定某个连续信号。Nyquist 采样定理告诉我们对带限信号以一定频率进行理想采样,即可保证该信号可以由采集而来的样本唯一确定。
连续时间信号 $\overset{采样}{\Longrightarrow}$ 离散时间信号 $\overset{量化、编码}{\Longrightarrow}$ 数字信号
采样的数学模型如下:
- 时域:$x_p(t)=x(t)\cdot p(t)$
- 频域:$X_p(j\omega)=\displaystyle\frac{1}{2\pi}X(j\omega)*P(j\omega)$
理想采样(冲激串采样),用周期为 $T$ 的冲激串 $p(t)=\displaystyle\sum_{n=-\infty}^\infty\delta(t-nT)=\displaystyle\sum_{n=-\infty}^\infty\frac{1}{T}e^{jk\omega_st}$ 对信号进行采样,则有:
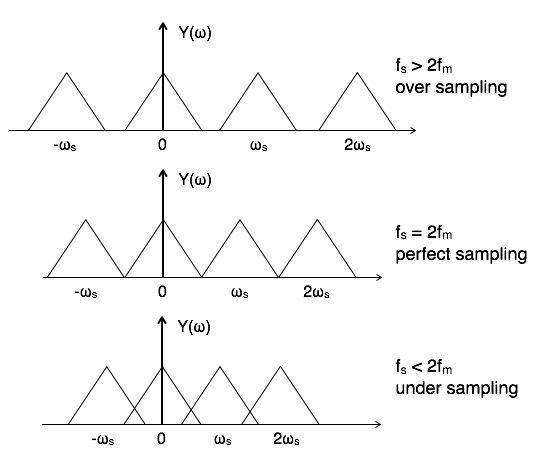
\[x_p(t)=\sum_{n=-\infty}^\infty x(nT)\delta(t-nT)=\sum_{n=-\infty}^\infty\frac{1}{T}x(t)e^{jk\omega_st}\] \[X_p(j\omega)=\frac{1}{2\pi}X(j\omega)*P(j\omega)=\frac{1}{T}\sum_{k=-\infty}^\infty X(j(\omega-k\omega_s))\]可以看出,在时域上对连续信号进行冲激串采样,就相当于在频域对信号以 $\omega_s=2\pi/T$ 为周期进行延拓(时域的离散化对应频域的周期化)。因此,采样频率 $\omega_s$ 决定了采样后的频谱是否会出现混叠情况,出现混叠则无法不失真的将其还原。因此我们要求:
- $X(j\omega)$ 为带限,带限于 $\omega_m$
- 采样频率满足 $\omega_s\geq2\omega_m$
- 滤波器的截止频率 $\omega_c$ 满足 $\omega_m<\omega_c<\omega_s-\omega_m$
零阶保持采样
零阶保持采样相当于理想采样后,再级联一个零阶保持系统:
\[h_0(t)=u(t)-u(t-T)\quad H_0(j\omega)=T\text{sinc}\frac{T\omega}{2\pi}e^{-j\omega T/2}\] \[x_0(t)=x_p(t)*h_0(t)=\sum_{n=-\infty}^\infty x(nT)h_0(t-nT)\]所以,信号 $x_0(t)$ 可看成是基本信号 $h_0(t)$ 的移位、加权、组合。为使信号能够不失真还原,该系统后面需要再级联一个系统 $H_r(j\omega)$ 以消除 $H_0(j\omega)$ 带来的影响,其满足 $H_r(j\omega)\cdot H_0(j\omega)=T$,截止频率满足采样定理。
信号的内插恢复
内插,即由样本值重建某一函数的过程。理想内插以理想低通滤波器的单位冲激响应 $h(t)$ ~ $\text{sinc}$ 作为内插函数,内插的输出即恢复的信号 $y(t)=h(t)*x_s(t)$
欠采样
频谱混叠会导致信号的失真,欠采样利用了混叠造成的影响,可以根据需要放缩信号的高频/低频信号。